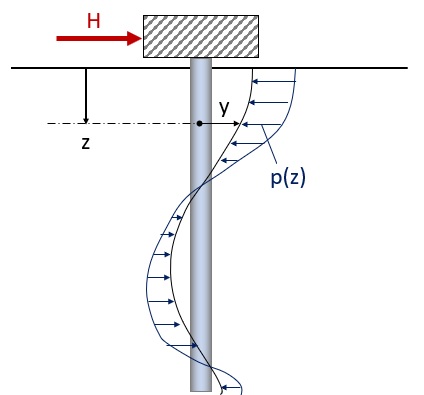
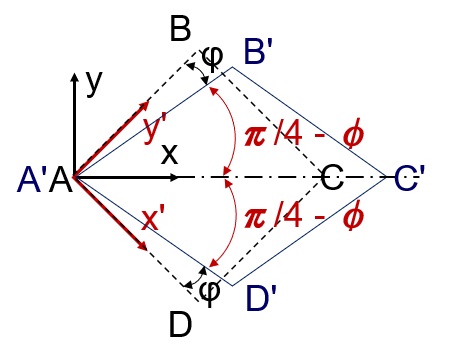
杭の設計や、地盤の応答変位計算をする際に、計算で直接必要な値が分からない場合や、定数同士の関係性を崩さずに、他の地盤について検討したいというときの参考となればと思い、この記事をまとめます。
※必ず引用元を記載します。
N値が0の場合、設計用の地盤定数はどう求めたらよいか・・・
例えばE0
$$E_{0}=2G(1+\nu)=2(1+\nu)\rho{V_{S}}^2$$
cuは?
$$c_{u}=0.5×q_{u}=0.5×(40+N)=20$$
といった計算方法があります。
VSが1.5倍になると・・・
$$G_{0}=\frac{\gamma_{t}}{g}{V_S}^2$$
の関係から、E0とGは1.5×1.5=2.25倍になると推定できます。
では、具体的な計算式をまとめていきます。
G0:土の初期せん断剛性の求めかた
$$G_{0}=\frac{\gamma_{t}}{g}{V_S}^2$$
G0:初期せん断剛性(kN/m2)
VS:せん断波速度(m/s)
γt:土の単位体積重量(kN/m3)
g:重力加速度(m/s“
※\(\frac{\gamma_{t}}{g}\)は密度\(\rho\)(kg/m3)で与えられている場合もあります。その場合は\(G_{0}=\rho{V_S}^2\)
引用元:『設計用地盤定数の決め方-土質編-』地盤工学会
PS検層の結果が無い場合のVSの求め方
$$V_{S}=80N^{\frac{1}{3}}(砂質土、N≦50)$$
$$V_{S}=100N^{\frac{1}{3}}(粘性土、2≦N≦50)$$
$$V_{S}=23{q_{u}}^{0.36}(粘性土、N<2)$$
N:標準貫入試験によるN値
qu:一軸圧縮強さ(kN/m2)
引用元:『道路橋示方書,Ⅴ耐震設計編』日本道路協会
ポアソン比νの求め方
$$\nu=\frac{1-2(\frac{V_{S}}{V_{P}})^2}{2(1-(\frac{V_{S}}{V_{P}})^{2})}$$
VS:せん断波速度(m/s)
VP:縦波速度(m/s)
引用元:『設計用地盤定数の決め方-土質編-』地盤工学会
初期変形係数E0の求め方
E0を算出する方法は2通りあります。
$$E_{0}=700N$$
E0:初期変形係数(kN/m2)
N:標準貫入試験によるN値
引用元:『建築基礎構造設計指針』日本建築学会
$$E_{0}=2G(1+\nu)=2(1+\nu)\rho{V_{S}}^2$$
引用元:『設計用地盤定数の決め方-土質編-』地盤工学会
せん断剛性Gの求め方
$$G=\frac{E}{2(1+\nu)}$$
引用元:フックの法則
土のせん断強さτfの求め方
$$\tau_{f}=c_{u}+\sigma・\tan{\phi}$$
τf:せん断強さ(kN/m2)
cu:粘着力(kN/m2)
σ:せん断面に垂直な応力(kN/m2)
φ:内部摩擦角(°)
N値による強度定数の推定値
| 推定式 | 備考 |
|---|---|
| qu=12.5N | Terzaghi&Peck |
| qu=40+N | 大崎 |
| cu=0.5×qu | クーロン |
| \(φ=\sqrt{15N}+15\) | 国交省 |
| \(φ=\sqrt{20N}+15\) | 大崎 |
qu:粘性土の一軸圧縮強さ(kN/2)
cu:粘着力(kN/2)
φ:内部摩擦角(°)
引用元:『使える土木工学』山海堂
変形係数Eの関係式
$$E_P=700N$$
$$E_S=3E_P=3E_C=2100N$$
EP:孔内水平載荷試験から得られる変形係数
ES:平板載荷試験から得られる変形係数
EC:一軸、三軸圧密試験から得られる変形係数
引用元:『設計用地盤定数の決め方-土質編-』地盤工学会
以上、他にもまだまだありますが、今回はここまでとします。