PΔ効果とは?
PΔ効果とは、構造計算において、軸力を受ける鉛直部材が水平方向に大きな変形を生じた際に、軸力と水平変位により付加曲げモーメントの影響を受ける効果のことを言います。
構造計算においては、微小変形理論により減少を捉える計算が多いため、PΔ効果のような大変形時の幾何学的非線形性を考慮しない場合、危険側に評価してしまう可能性があります。
幾何学的非線形を考慮するとP⊿効果が表れる
微小変形理論を前提とする計算では、大変形による幾何学的非線形は無視されます。
しかし、構造計算ソフトの荷重増分解析により、保有水平耐力を計算する際、崩壊形を確認する必要がありますが、崩壊形を確認するためには、水平方向に大きな変形をさせないと部材に降伏ヒンジが生じない場合があります。
水平方向に大きな変形をした場合、建物の自重と変形による負荷水平力が、無視できないほど大きくなることが考えられます。
この場合は、幾何学的非線形を考慮した応力の算定が必要と考えられます。
P⊿効果のイメージ
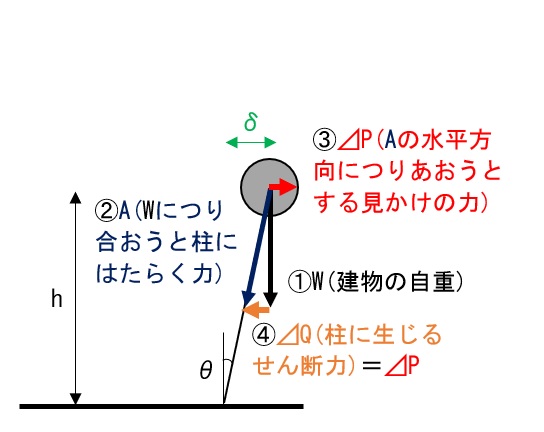
図のように、水平方向へδ変形した場合、自重Wによって、柱の軸と、ずれた(ななめ)方向へ力が働くことになります。
このななめ方向の力に、見かけの水平方向の力⊿Pを加えないと、全体の力がつりあいません。
つまり、柱に、ななめ方向の水平方向成分、せん断力⊿Qが働きます。
P⊿効果により付加されるせん断力⊿Qは、次式のように表すことができます。
$${⊿P}={⊿Q}={W×θ}={W}×\frac{{δ}}{{h}}$$
地震力によって生じる層せん断力
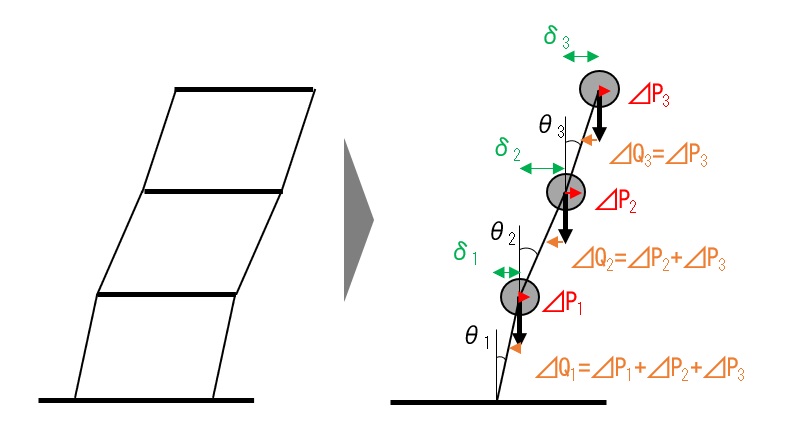
地震による層せん断力Qiは、地震層せん断力係数Ciと各層の重さWiで表すと、下式になります。
$${Q}_{i}={C}_{i}×\sum_{j=i}^{n}{W_{j}}$$
地震による層せん断力Qiは、層せん断力係数Ciにその層より上の建物自重Wを加えた値を乗じたものとなります。
P⊿効果による⊿Qを層せん断力係数⊿Cの形で表す
⊿Cを、\({⊿Q}={W×θ}={W}×\frac{{δ}}{{h}}\)という式と比較して表すと
$${⊿C}=\frac{{⊿Q}}{{W}}=\frac{{δ}}{{h}}$$
となり、P⊿効果による層せん断力係数の負荷分は、層間変形角θ(R)そのものになります。
P⊿効果の大きさ
増分解析を実施し、最終ステップ時の層間変形角R=1/30まで変形させたとします。
また、この時の構造特性係数Dsが0.3だったとします。
このDsに対する、P⊿効果による層せん断力係数⊿C=1/30の大きさは次のように表すことができます。
$$\frac{1/30}{0.3}=0.11{・・・}=11.1{%}$$
このように、幾何学的非線形を考慮し、R=1/30まで変形した場合の負荷水平力⊿Qは、Ds値に対して11.1%の大きさになることが分かります。
まとめ
保有水平耐力計算で、幾何学的非線形が考慮されているか、考慮されていないかを確認し、P⊿効果を見込んだ安全な設計をする必要があると考えられます。
他にも、スパンが大きくなるほど、変形が大きくなるという場合が考えられます。