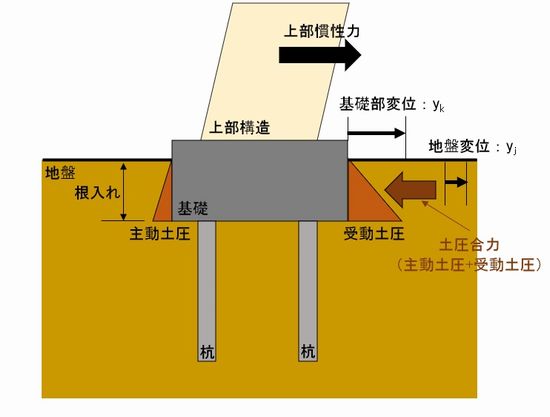
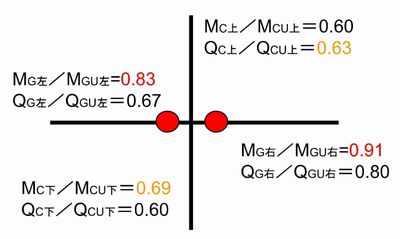
山留の側圧計算で用いるランキン・レザ―ル式の内容について触れていきたいと思います。
山留の側圧分布
山留の側圧は、下図のような分布形状をしています。
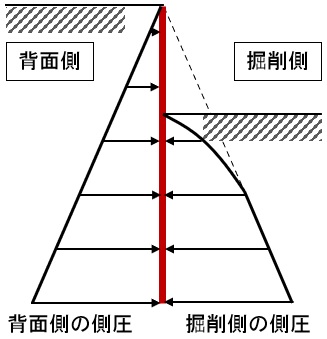
図の右側の掘っていく側を掘削側、左側を背面側と言います。
掘削を進めると、図のように背面側の側圧が大きくなるため、深いところまで掘る場合には切梁という、つっかえ棒を山留に設置します。
ランキン・レザ―ル式
山留の側圧を計算で求める式には、いくつかありますが、代表例としてランキン・レザール式をご紹介します。
ランキン・レザ―ル式は背面側と掘削側で、計算式が少しだけ異なります。
背面側のランキン・レザ―ル式
$$P_{a}=(\gamma_{t}{z}-{P}_{wa})\tan^2{(\frac{\pi}{4}-\frac{\phi}{2})}-2{c}\tan{(\frac{\phi}{4}-\frac{\phi}{2})}+P_{wa}$$
Pa:地表面からの深さz(m)における背面側の側圧(kN/m2)
γt:土の湿潤単位体積重量(kN/m3)
z:地表面からの深さ(m)
Pwa:地表面からの深さz(m)における背面側の水圧(kN/m2)
c:土の粘着力(kN/m2)
φ:土の内部摩擦角(°)
掘削側のランキン・レザ―ル式
$$P_{P}=(\gamma_{t}z_{P}-P_{wP})\tan^2{(\frac{\pi}{4}+\frac{\phi}{2})}+2{c}\tan{(\frac{\phi}{4}+\frac{\phi}{2})}+P_{wP}$$
PP:根切底面からの深さzp(m)における掘削側の側圧の上限値(kN/m2)
γt:土の湿潤単位体積重量(kN/m3)
zP:根切り底面からの深さ(m)
PwP:根切り底面からの深さzP(m)における掘削側の水圧(kN/m2)
c:土の粘着力(kN/m2)
φ:土の内部摩擦角(°)
モール・クーロン式からの導出
モール・クーロン式の考え方

モール・クーロン式は、モールの応力円とクーロンの強度式の2式から成り立っています。
モールの応力円
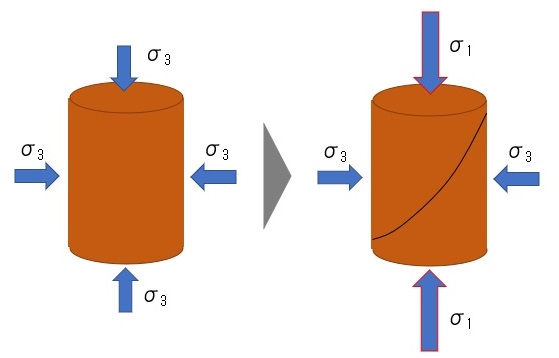
モールの応力円は、最小主応力(σ3)と最大主応力(σ1)から、主応力とせん断力の関係を表した図です。
主応力とせん断力の組合わせによる、土の強度曲線を描いています。円の外側に行くと破壊するというイメージです。
クーロンの強度式
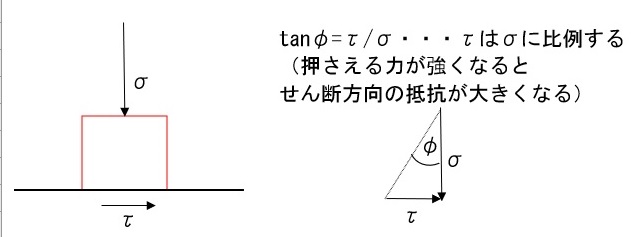
クーロンの強度式は、土のすべり強度を表す式です。土のすべり強度は、摩擦力に似ていて、圧力をかけた状態の方がすべり強度が増すので、右肩上がりの直線になっています。
ここで、cは全く圧力を掛けないでもある程度はすべり強度があるということを表しています。
砂は、圧力を加えるとすべり強度が増しますが、粘土は圧力を加えても変形してしまうため、比例関係とはせずに、圧力が加わっても粘着力のみを強度と考えています。
クーロンの強度式は、図から次のように表すことができます。
$$\tau=\tan{\phi}{×}\sigma+c$$
(※y=ax+b の一次方程式の形です。(y=τ、x=σ、a=tanφ、b=c))
ランキン・レザ―ル式の導出
ランキン・レザ―ル式は背面側の圧力が小さくなる方は最小主応力(図のσ3)を、掘削側の圧力が大きくなる方は最大主応力(図のσ1)を計算で求めていきます。

まずは、モールの応力円とクーロン強度式の接線が交わる点D(σf,σ<τf)の座標を、σ1,σ3,φで表します。
σ1,σ3の中点をσ2,A=Bsinφより
$$\begin{eqnarray}
\sigma_{f} &=& \sigma_{2}-{B}\sin{\phi} \\
&=& \frac{\sigma_{1}+\sigma_{3}}{2}-\frac{\sigma_{1}-\sigma_{3}}{2}\sin{\phi}
\end{eqnarray}$$
τf=Bcosφより
$$\tau_{f}=\frac{\sigma_{1}-\sigma_{3}}{2}\cos{\phi}$$
つぎに、クーロンの強度式にσfとτfを代入します。
$$\frac{\sigma_{1}-\sigma_{3}}{2}\cos{\phi}=\tan{\phi}\{\frac{\sigma_{1}+\sigma_{3}}{2}-\frac{\sigma_{1}-\sigma_{3}}{2}\sin{\phi}\}+{c}$$
\(\tan{\phi}=\frac{\sin{\phi}}{\cos{\phi}}\)とし、整理すると
$$\sigma_{3}(1+\sin{\phi})=\sigma_{1}(1-\sin{\phi})-2{c}\cos{\phi}{・・・式1}$$
背面側の側圧計算
背面側は、圧力が小さくなり、土が破壊することを考えると、最少主応力σ3の式を導出すれば良さそうです。
式1をσ3の等式にします。
$$\sigma_{3}=\sigma_{1}\frac{1-\sin{\phi}}{1+\sin{\phi}}-2{c}\frac{\cos{\phi}}{1+\sin{\phi}}$$
ここで、三角形の合成公式より
$$\tan^2{(\frac{\pi}{4}-\frac{\phi}{2})}=\frac{1-\sin{\phi}}{1+\sin{\phi}}$$
また、右辺の分母と分子に(1+sinφ)を掛け、両辺を1/2乗すると
$$\tan{(\frac{\pi}{4}-\frac{\phi}{2})}={±}\sqrt{\frac{1-\sin^2{\phi}}{(1+\sin{\phi})^2}}$$
ここで、図の上半分だけの範囲を考え、右辺の分母1-sin2φ=cos2φと変形すると
$$\tan{(\frac{\pi}{4}-\frac{\phi}{2})}=\frac{\cos{\phi}}{1+\sin{\phi}}$$
σ3の式にこれらの結果を代入すると
$$\begin{eqnarray}
\sigma_{3} &=& \sigma_{1}\frac{1-\sin{\phi}}{1+\sin{\phi}}-2{c}\frac{\cos{\phi}}{1+\sin{\phi}}\\
&=& \sigma_{1}\tan^2{(\frac{\pi}{4}-\frac{\phi}{2})}-2{c}\tan{(\frac{\pi}{4}-\frac{\phi}{2})}
\end{eqnarray}$$
背面側のランキン・レザ―ル式とモール・クーロン式の関連性
背面側のモール・クーロン式は
$$\sigma_{3}=\sigma_{1}\tan^2{(\frac{\pi}{4}-\frac{\phi}{2})}-2{c}\tan{(\frac{\pi}{4}-\frac{\phi}{2})}$$
背面側のランキン・レザ―ル式は
$$P_{a}=(\gamma_{t}z-P_{wa})\tan^2{(\frac{\pi}{4}-\frac{\phi}{2})}-2{c}\tan{(\frac{\phi}{4}-\frac{\phi}{2})}+P_{wa}$$
水圧はそのまま側圧としてかかりますので、Pwaです。
σ1は土圧-水圧として考えますので、\((\gamma_{t}z-P_{wa})\)です。
掘削側も同様に計算式をひも解いていけます。背面側では、最少主応力σ3について解きましたが、掘削側では最大主応力σ1について解きます。
以上、ランキン・レザ―ル式の導出をしました。参考にしてください。