【コンクリートの収縮ひび割れ予測】修正ベース・マレー法

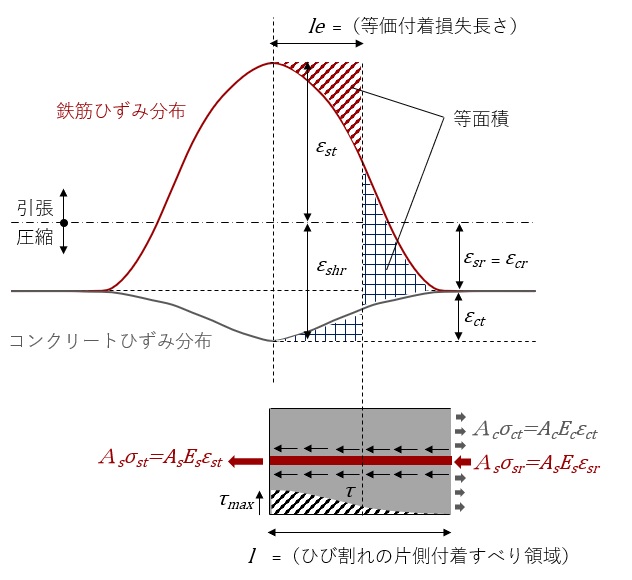
上の図はひび割れが発生する箇所の鉄筋コンクリート造の断面を模式的に表しています。

断面の左右方向の力の釣合を考えると

$$A_s\sigma_{st}-A_s\sigma_{sr}=A_c\sigma_{ct}=l_e U \tau_{max}$$
A_s:鉄筋の断面積
A_c:コンクリートの断面積
σ_st,σ_sr:鉄筋応力
σ_ct:コンクリート応力
τ_max:付着強度
U:鉄筋周長
ここに$U=4\frac{A_s}{d_b}$
d_b:鉄筋径

ひび割れが発生するとひび割れ位置の鉄筋ひずみはε_st（山の頂点）となります。また、ひび割れに近い部分のコンクリーとのひずみは、ε_shrとなります。
ひび割れ幅は、上図の鉄筋ひずみとコンクリートひずみの２つの曲線で囲まれる部分の面積に相当します。同図の網掛け部分の面積が等しくなるように長さlを定義すると、等価付着損失長さl_e（鉄筋とコンクリートの付着が無くなっていると考える部分）は次式となります。

$$l_e=\frac{\sigma_{ct}}{4 \tau_{max}}・\frac{d_b}{\rho} $$

収縮ひび割れ幅w（mm）は次式となります。

$$w=2l_e(\varepsilon_{st}+\varepsilon_{shr})=2l_e(\frac{\sigma_{st}}{E_s}+\varepsilon_{shr})$$

ε_st:ひび割れ面の鉄筋ひずみ
E_s:鉄筋のヤング係数
ε_shr:コンクリートの収縮ひずみ

修正ベース・マレーの式

引張破断強度$\sigma_{ct}$と付着強度$\tau_{max}$が比例関係にあるとみなすと、定数αを用いてl_eを簡易式で表すことが出来ます。
また、クリープ(残留）変形を考慮した低減係数bと、拘束度λを考慮することで、以下の４式が得られます。

$$l_e=\alpha\frac{d_b}{\rho}$$
$$w=2l_e(\frac{\sigma_{st}}{E_s}+\frac{\lambda \varepsilon_{shr}}{b})$$
$$m=1+\frac{Ln\rho}{2l_e}(\frac{\lambda \varepsilon_{shr}- \varepsilon_{ct}}{b \varepsilon_{ct}})$$
$$\sigma_{st}=E_s(\frac{\lambda \varepsilon_{shr}-\varepsilon_{ct}}{b} + \varepsilon_{ct})・(\frac{L-2ml_e}{Ln \rho +2ml_e})$$