線膨張係数とは?
温度の上昇に対応して、長さが変化する割合を線膨張率(線膨張係数)と言います。
このページでは、主任技士の過去問で出題された、線膨張係数に関する問題をご紹介します。
コンクリートの線膨張係数は覚えていますか?覚えていないと解けない問題ですので、この記事を参考に、一回で覚えてしまってください。
コンクリート主任技士過去門 平成28年No.13
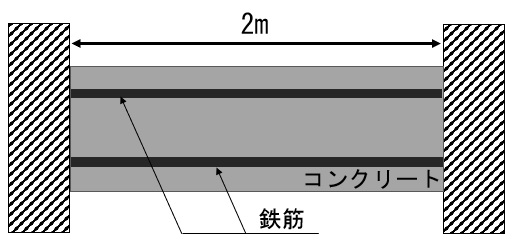
下図のような両端を完全に固定した長さ2mの鉄筋コンクリート梁の温度が下記の条件で一様に10℃上昇した。この時、コンクリートに生じる応力に関する次の記述のうち、適当なものはどれか。
(条件)
梁にひび割れは発生していないものとする。
コンクリートのヤング係数は2.5×104N/mm2とする。
鉄筋とコンクリートの線膨張係数は同一とする。
コンクリートのクリープの影響は無視する。
温度上昇の前の初期応力は0とする。
(1)約2.5N/mm2の引張応力が発生する。
(2)約2.5N/mm2の圧縮応力が発生する。
(3)約5.0N/mm2の引張応力が発生する。
(4)約5.0N/mm2の圧縮応力が発生する。
回答
コンクリート主任技士試験を主催している、日本コンクリート工学会から「鉄筋とコンクリートの線膨張係数は覚えておいてね」というメッセージを感じる問題です。
線膨張係数
線膨張率や熱膨張係数、体積膨張係数とも呼ばれます。ある部材が1℃の温度変化をしたときのひずみのことです。
あえて、ひずみと強調したのは、「長さ変化」と表現してしまうと混乱してしまうためです。
厳密には、温度によって線膨張係数は異なります。例えば超低温化と超高温下では線膨張係数は異なります。しかし、建築の構造分野では、常温化のある一定の線膨張率を採用することが通常です。
コンクリートと鉄筋の線膨張係数はほぼ等しく以下のようになります。
コンクリートの線膨張係数=1.0×10-5(/℃)
この値は、覚えなければならないということです。
ひずみ(ε)
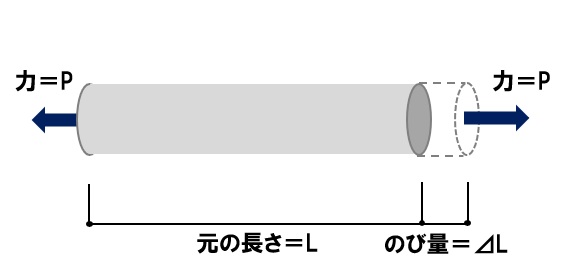
ひずみの定義を思い出してください。ある長さ(L)の部材が長さ変化(δL)をしたとき、ひずみ(ε)は下の式のように表します。
$$\varepsilon=\frac{\delta{L}}{L}$$
ひずみ(ε)と応力(σ)の関係
応力は、単位面積当たりにかかる力(単位の例:N/mm2)のことを言います。フックの法則(ばねののびと復元力の関係)と同じように、「単位面積あたり」では下の式が成り立ちます。
$$\sigma={E}\varepsilon$$
E:ヤング係数
以上を踏まえて、問題を見ていきます。問題図には、「2m」と記載されています。この数値を見てしまうと、迷ってしまう可能性があります。無視しましょう。
なぜならば、問題文では「コンクリートに生じる応力」に関して問われているからです。
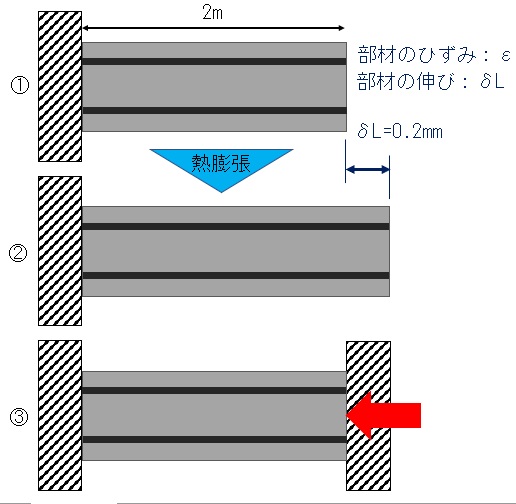
自由膨張した場合、図の①から②のように、部材がのびますが、問題では③のように両側が固定されるため、部材に内部には、ひずんだ(のびた)分だけ縮めようとする応力(圧縮応力)が内部に働くことになります。
問題では、10℃の温度上昇ですので、ひずみの計算方法は以下のようになります。
$$10×(1.0×10^{-5})=1.0×10^{-4}$$
このひずみを縮めようとする応力の計算は
$$\sigma=(2.5×10^4)×(1.0×10^{-4})$$
σ=2.5、答えは(2)の2.5N/mm<sup>2</sup>となります。
以上、過去問から学べることは多いですね!