$$E=2(1+\nu)G{ , }G=\frac{E}{2(1+\nu)}$$
応力(σ)ひずみ(ε)関係とポアソン比(ν)
$$\nu=\left|\frac{\epsilon_{x}}{\epsilon_{y}}\right|$$
$$\epsilon_{x}=\frac{\sigma_{x}}{E}$$
$$\sigma_{y}={E}\epsilon_{y}=-\nu\epsilon_{y}{→}\epsilon_{y}=-\nu\frac{\sigma_{y}}{E}$$
$$\epsilon_{x}=\frac{1}{E}\left(\sigma_{x}-\nu\sigma_{y}\right){・・・式1}$$
ヤング係数(E)せん断弾性係数(G)の関係
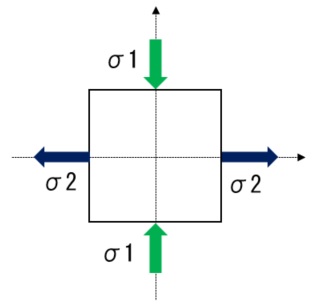
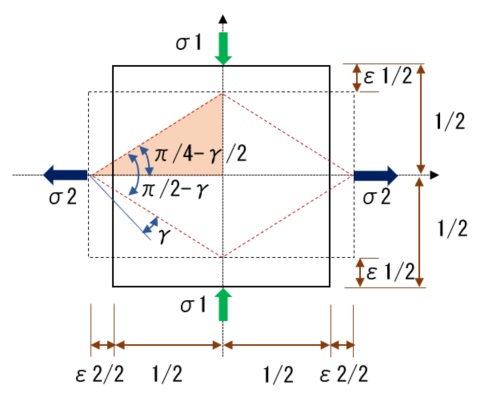
$$\epsilon1=\epsilon2(=\epsilon)$$
$$\frac{\frac{1}{2}-\frac{\epsilon}{2}}{\frac{1}{2}+\frac{\epsilon}{2}}=\tan{{(\frac{\pi}{4}-\frac{\gamma}{2})}}$$
$$\epsilon=\frac{\gamma}{2}{・・・式2}$$
ちょっと詳しく解説
$$\begin{eqnarray}\frac{\frac{1}{2}-\frac{\epsilon}{2}}{\frac{1}{2}+\frac{\epsilon}{2}} &=& \frac{{(\frac{1}{2}-\frac{\epsilon}{2})}^2}{\frac{1}{2}+\frac{\epsilon}{2}{(\frac{1}{2}-\frac{\epsilon}{2})}}\\
&=& \frac{\frac{1}{4}-\frac{\epsilon}{2}+\frac{\epsilon^2}{4}}{\frac{1}{4}-\frac{\epsilon^2}{4}}\\
&=& 1-2\epsilon
\end{eqnarray}$$
$$\begin{eqnarray}\tan{{(\frac{\pi}{4}-\frac{\gamma}{2})}} &=& \frac{\tan{\frac{\pi}{4}}-\tan{\frac{\gamma}{2}}}{1+\tan{\frac{\pi}{4}}\tan{\frac{\gamma}{2}}}\\
&=& \frac{1-\frac{\gamma}{2}}{1+\frac{\gamma}{2}}\\
&=& \frac{{(1-\frac{\gamma}{2})}^2}{{(1+\frac{\gamma}{2})}{(1-\frac{\gamma}{2})}}\\
&=& \frac{1-\gamma+\frac{\gamma^2}{4}}{1-\frac{\gamma^2}{4}}\\
&=& 1-\gamma
\end{eqnarray}$$
※圧縮のσ1を正としているのは、後の計算をしやすくするためです。
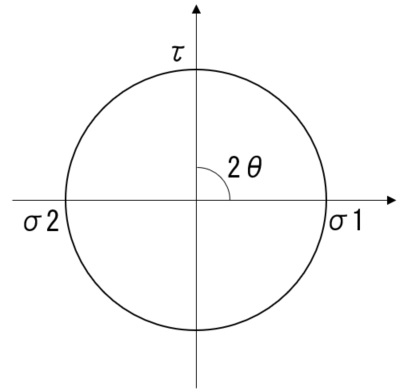
$$\epsilon_{x}=\frac{1}{E}\left(\sigma_{x}-\nu\sigma_{y}\right){・・・式1}$$
$$\frac{\gamma}{2}=\frac{1}{E}\left(\tau-\nu\tau\right)$$
$$E=2(1+\nu)G{ , }G=\frac{E}{2(1+\nu)}$$