(RC部材の)トラス機構とは
トラス機構とは、RC柱・梁部材にせん断力を加えたときの、せん断力の内部伝達をモデル化したものです。
トラス機構とともに、アーチ機構がありますが、このページでは、トラス機構についてのみイメージをお伝えできればと思います。
トラス・アーチ機構の式
柱および梁のせん断信頼強度\(V_{u}\)は次の3式による値のうちの最小値とします。
$$\begin{eqnarray}
V_{u} &=& \mu{p}_{we}\sigma_{we}b_{e}j_{e}+(\nu\sigma_{b}-\frac{5p_{we}\sigma_{wy}}{\lambda})\frac{bD}{s}\tan{\theta} {・・・式1} \\
\\
V_{u} &=& \frac{\lambda\nu\sigma_{B}+p_{we}\sigma_{we}}{3}b_{e}j_{e} {・・・式2} \\
\\
V_{u} &=& \frac{\lambda\nu\sigma_{B}}{2}b_{e}j_{e} {・・・式3}
\end{eqnarray}$$
式の構成
式1の第2項、式2、式3はトラス機構の式を表しています。
式1の第1項はアーチ機構の式を表しています。Vuはせん断耐力です。
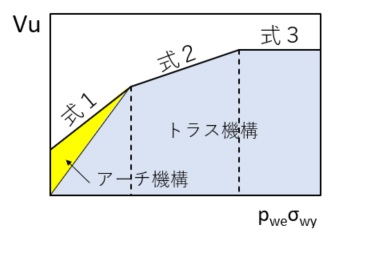
トラス・アーチ機構のイメージ図と式の関係
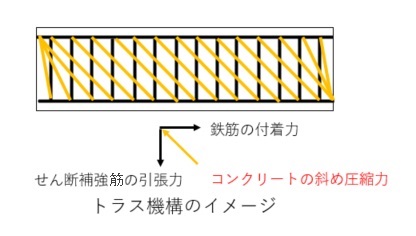
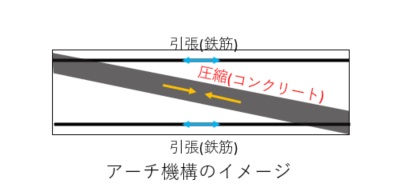
トラス機構は、鉄筋の付着力とせん断補強筋の引張力、コンクリートの斜め圧縮力が図のようにつりあう状態を表しています。
$$\begin{eqnarray}
& &(\nu\sigma_{b}-\frac{5p_{we}\sigma_{wy}}{\lambda})\frac{bD}{s}\tan{\theta}\\
\\
& &\frac{\lambda\nu\sigma_{B}+p_{we}\sigma_{we}}{3}b_{e}j_{e}\\
\\
& &\frac{\lambda\nu\sigma_{B}}{2}b_{e}j_{e}
\end{eqnarray}$$
アーチ機構は、部材全体が応力に対して抵抗している状態を表しています。
$$\mu{p}_{we}\sigma_{we}b_{e}j_{e}$$
トラス機構の応力のつりあいと式
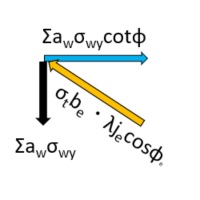
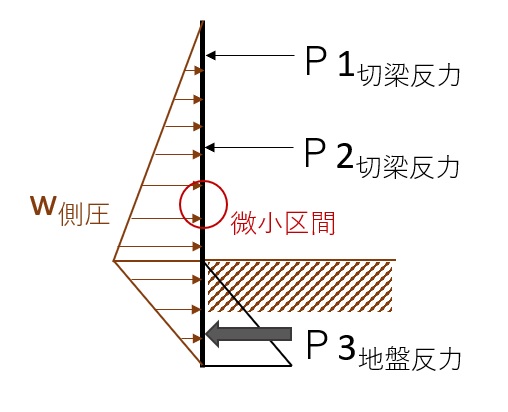
トラス機構では、図のように、3方向の力のつりあいを考えます。
水平方向:主筋の付着力
垂直方向:せん断補強筋の耐力
斜め方向:コンクリートの圧縮力
これらのつりあいを考えると、次の式が得られます。
$${(\Sigma{a}_{w}\sigma_{w})}^2{(1+\cot^2{\phi})}={(\sigma_{t}{b}_{e}\lambda{j}_{e}\cos{\phi})}^2{・・・式4}$$
トラス機構が負担するせん断耐力Vt
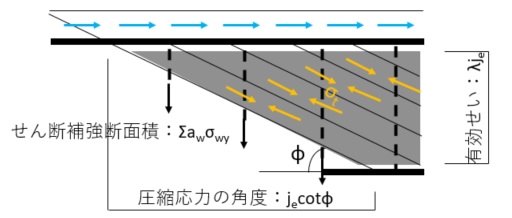
垂直方向のせん断補強筋の耐力の合計はコンクリートの斜め圧縮力が横切る、せん断補強筋の耐力の合計とします。
$${V}_{t}=\Sigma{a}_{w}{\sigma}_{wy}={p}_{we}{\sigma}_{wy}{b}_{e}{j}_{e}{\cot{\phi}}{・・・式5}$$
σwy:せん断補強筋の降伏耐力
pwe:せん断補強筋比
bejecotφ:圧縮力が横切るせん断補強筋の断面積
トラス機構の基本式
式4を式5に代入します。ここで
$${(\frac{\cot{\phi}}{\cos{\phi}})}^2=\frac{1}{\sin^2{\phi}}=1+\cot^2{\phi}$$
を利用して整理します。
$$1+\cot^2{\phi}=\frac{\lambda\sigma_{t}}{p_{we}\sigma_{wy}}{・・・式6}$$
σt:コンクリートの斜め圧縮応力です。トラス機構の式はコンクリートが圧縮破壊を起こさないことを前提としていますので、コンクリートの圧縮強度をν0σBを超えないことを考慮すると、式6は次のように表すことができます。
$$1+\cot^2{\phi}=\frac{\lambda\sigma_{t}}{p_{we}\sigma_{wy}}{≦}\frac{\lambda\nu_{0}\sigma_{B}}{p_{we}\sigma_{wy}}$$
$$\cot{\phi}{≦}\sqrt{\frac{\lambda\nu_0\sigma_{B}}{p_{we}\sigma_{wy}-1}}{・・・式7}$$
トラス機構によるせん断力負担
式5に式6と式7を代入すると、トラス機構のせん断力負担は、次式のうち、最小値で与えられます。
$$\begin{eqnarray}
{V}_{T} &=& 2{p}_{we}\sigma_{wy}{b}_{e}{J}_{e}{・・・式8}\\
\\
{V}_{t} &=& {p}_{we}\sigma_{wy}{b}_{e}{j}_{e}\sqrt{\lambda\nu_{0}\sigma_{B}}{p_{we}\sigma_{wy}}-1{・・・式9}
\end{eqnarray}$$
これらをグラフで表すと、次のようになります。
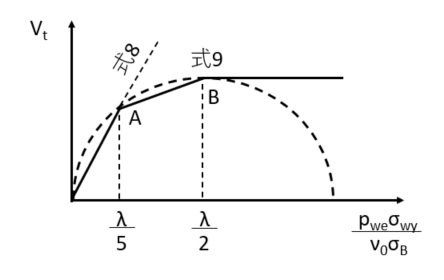
点Aの導出方法
式8は、式7にcotφ=2を代入することで得られます。
これは、cotφは大きくなるほど応力伝達が困難になるため、cotφ=2が上限とされていることによります。cotφ=2ということは、逆数であるtanφ=0.5です。このとき、角度でいうとφ=約26°となります。
$$\begin{eqnarray}
\cot{\phi} & {≦}& \sqrt{\frac{\lambda\nu_{0}\sigma_{B}}{p_{we}\sigma_{wy}-1}}\\
\\
2 &{≦}& \sqrt{\frac{\lambda\nu_{0}\sigma_{B}}{p_{we}\sigma_{wy}-1}}\\
\\
5 &{≦}& \frac{\lambda\nu_{0}\sigma_{B}}{p_{we}\sigma_{wy}}\\
\\
\frac{\lambda}{5} &{≦}& \frac{\nu_{0}\sigma_{B}}{p_{we}\sigma_{wy}}
\end{eqnarray}$$
点Bの導出方法
式9を変形させると、円を表す式となります。
$$\begin{eqnarray}
{V}_{t} &=& {p}_{we}\sigma_{wy}{b}_{e}{j}_{e}\sqrt{\lambda\nu_{0}\sigma_{B}}{p_{we}\sigma_{wy}}-1\\
\\
\frac{{{V}_{t}}^2}{({{p}_{we}\sigma_{wy}{b}_{e}{j}_{e})}^2} &=& \frac{\lambda\nu_{0}\sigma_{B}}{p_{we}\sigma_{wy}}-1
\end{eqnarray}$$
ここで、のちに円のグラフで表しやすくするために、式を変形させます。
$${V_{t}}^2+{(\nu_{0}\sigma_{B}{b}_{e}{j}_{e})}^2{(\frac{p_{we}\sigma_{wy}}{\nu_{0}\sigma_{B}})}^2={(\nu_{0}\sigma_{B}{b}_{e}{j}_{e})}^2\frac{\lambda{p_{we}\sigma_{wy}}}{\nu_{0}\sigma_{B}{b}_{e}{j}_{e}}$$
ここで、\({(\nu_{0}\sigma_{B}{b}_{e}{j}_{e})}^2\)を\(\alpha\)とおきます。
$${V_{t}}^2+{\alpha}^2{(\frac{p_{we}\sigma_{wy}}{\nu_{0}\sigma_{B}})}^2={\alpha}^2{\frac{\lambda{p_{we}\sigma_{wy}}}{\nu_{0}\sigma_{B}{b}_{e}{j}_{e}}}$$
さらに、\(\frac{p_{we}\sigma_{wy}}{\nu_{0}\sigma_{B}}=x\)、\(V_{t}=y\)とおくと
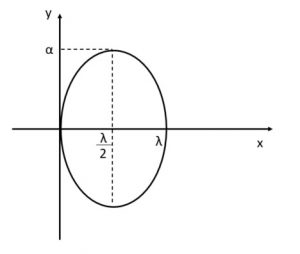
$${y}^2={\alpha}^2x{(\lambda-x)}$$
と表すことができます。この式は、x=0,1のときy=0、x=λ/2のときyは最大と最少をとるだ円を表す式です。