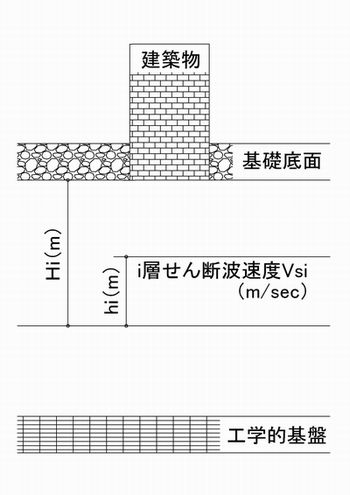
カステリアーノの定理を用いて、先端集中荷重と、分布荷重による、片持ち梁の部材先端の、たわみ角θの違いをみていきます。
少しだけカステリアーノの定理について
カステリアーノの定理は、構造物のエネルギーに着目して、構造物の応力および変形を求める方法です。
外力によって生じるエネルギー
外力エネルギーをWeとおくと、一定の外力Pが作用し、その点の外力方向に生じる変位をδとしたとき、Weは次式で表せられます。
$$We=Pδ$$
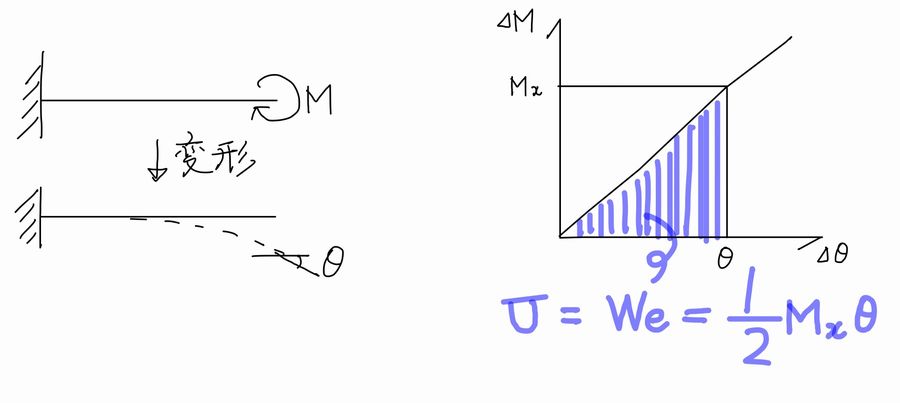
同様にして、作用外力モーメントとして曲げモーメントMが作用するとき、作用点に生じる回転角をθとすると、その外力エネルギーWeは次式で表せられます。
$$We=Mθ$$
内力(応力)によって生じるエネルギー
構造物の変形は外力によって構造物に生じる応力(内力)に対し各部がひずむことによって生じます。内力エネルギーをUとおくと、Uは構造物内部に蓄えられたひずみエネルギーをあらわすことになります。
エネルギーの保存則
外力が与えるエネルギー=内力が蓄えるエネルギー
$$We=U$$
カステリアーノの定理によると、長さLの部材に曲げモーメントMxがはたらいているとき、そのたわみ角は下式であらわせます。
$$θx=\int_0^L\frac{M_xM_x’}{EI}dx$$
$$M_x’=\frac{\partial Mx}{\partial M}$$
(a)先端集中荷重Pによるたわみ角θa VS (b)分布荷重ωによるたわみ角θb
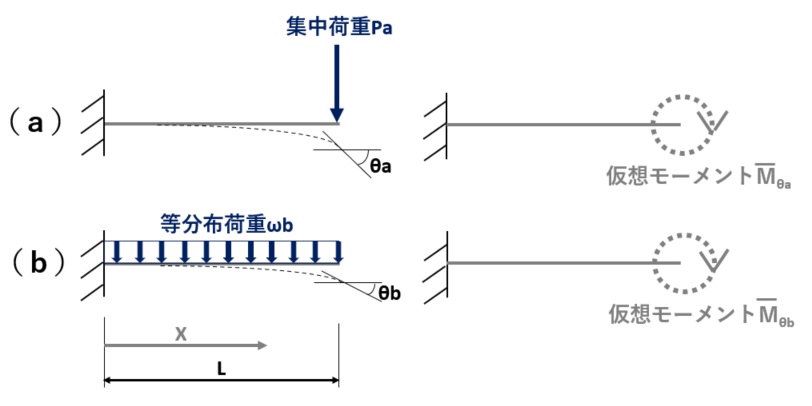
<準備計算>
知りたい場所のたわみ角を求めるためには、そのたわみ角が生じる場所に仮想の曲げモーメントMを与え、そのモーメントの仕事(仮想曲げモーメントM×たわみ角θ)を求めます。
まずは(a)の曲げモーメントの式
$$M_{xa}=-Px+\overline{M}$$
$$M_{xa}’=\frac{\partial M_{xa}}{\partial \overline{M}}=1$$
(b)の曲げモーメントの式
$$M_{xb}=\frac{ω}{2}x^2-ωLx+\overline{M}$$
$$M_{xb}’=\frac{\partial M_{xb}}{\partial \overline{M}}=1$$
<(a)集中荷重のたわみ角の式>
$$\begin{eqnarray}
θa &=&\int_0^L\frac{(-Px+\overline{M})・1}{EI}dx \\
&=&-\frac{PL^2}{2EI}
\end{eqnarray}$$
<b分布荷重のたわみ角の式>
$$\begin{eqnarray}
θb &=&\int_0^L\frac{(\frac{ω}{2}x^2-ωLx+\overline{M})・1}{EI}dx \\
&=&-\frac{ωL^3}{3EI}
\end{eqnarray}$$
ここで、\(ωL=P\)とおくと、
$$θb=-\frac{PL^2}{3EI}$$
分布荷重の合計を集中荷重の大きさPと合わせるためにωL=Pとおきましたが、結果、集中荷重の方が分布荷重に比べて1.5倍のたわみ角となることが分かりました。感覚的にわからない場合は、計算で確かめる必要があると改めて感じました。