余耐力法とは?
余耐力法とは、保有耐力計算において崩壊系が形成されなかった部分において、部材の残りの耐力から崩壊系を想定し、建物の保有水平耐力を推定する計算方法です。
余耐力法の計算例は、ページ下部にあります。
このページでは、保有水平耐力計算における課題と、余耐力法の計算例方法および計算例について、順を追ってご紹介します。
保有水平耐力と必要保有水平耐力
建築物のルート3による構造設計では、保有水平耐力(Qu)が必要保有水平耐力(Qun)以上であることを確認する必要があります。
Qu≧Qun
必要保有水平耐力
必要保有水平耐力の算定では、構造特性係数Dsを算出しなければなりません。
Qun=Ds・Fes・Qud
Qun:各階の必要保有水平耐力
Ds :構造特性係数
Fes:形状係数
Qud:各階の水平力
構造特性係数
構造特性係数(Ds)は、各階の柱・梁・壁部材の部材種別から算定されます。
例:柱・梁の種別
(※このページでは、分かりやすくするために純ラーメン構造を対象とします。)
1.Dsと部材群の種別
| 柱及び梁の部材群としての種別 | Dsの数値 |
| A | 0.3 |
| B | 0.35 |
| C | 0.4 |
| D | 0.45 |
2.部材群の種別と部材の耐力の割合
ここの検討では、各階の柱の部材種別の割合を算定しています。
| 部材の耐力の割合 | 部材群としての種別 | |
| (1) | γA≧0.5かつγC≦0.2 | A |
| (2) | γC<0.5(部材群としての種別がAの場合を除く。) | B |
| (3) | γC≧0.5 | C |
γA:種別FAである柱の耐力の和をFD以外のすべての柱の水平耐力(FA+FB+FC)で除した数値
(\(γ_{A}=\frac{{FA}}{{FA+FB+FC}}\))
γC:種別FAである柱の耐力の和をFD以外のすべての柱の水平耐力(FA+FB+FC)で除した数値
(\(γ_{C}=\frac{{FC}}{{FA+FB+FC}}\))
3.柱及び梁の部材種別
部材種別は、Ai分布に基づく外力分布を用いた増分解析により、建築物の崩壊形を確認し、崩壊形に達する場合の応力状態に基づき定めます。
つまり、崩壊形が形成されないと、部材種別が決定できないということになります。
(※ここで余耐力法が使われます。)
| 柱及び梁の区分 | 柱及び梁の種別 | ||||||
| 部材 | 柱及び梁 | 柱 | 梁 | ||||
| 条件 | 破壊の形式 | h0/Dの 数値 |
σ0/Fcの 数値 |
Ptの 数値 |
τu/Fcの 数値 |
τu/Fcの 数値 |
|
| せん断破壊、 付着割裂破壊、 圧縮破壊などの 脆性破壊を 生じないこと。 |
2.5以上 | 0.35以下 | 0.8以下 | 0.1以下 | 0.15以下 | FA | |
| 2.0以上 | 0.45以下 | 1.0以下 | 0.125以下 | 0.2以下 | FB | ||
| – | 0.55以下 | – | 0.15以下 | – | FC | ||
| FA、FB又はFCのいずれにも該当しない場合 | FD | ||||||
h0:柱の内のり高さ(cm)
D:柱の幅(cm)
σ0:崩壊形形成時の柱断面に生じる軸方向応力(N/mm2)
Pt:引張鉄筋比(%)
Fc:コンクリート強度(N/mm2)
τu:崩壊形形成時の柱断面に生じる平均せん断応力度(N/mm2)
余耐力法の計算方法
1.増分解析結果の参照
増分解析を実施したとして、最大層間変形角が1/30になった場合でも、高層建物の上層階はヒンジを生じない接合部が残る場合が多いです。
下の図のように、増分解析を行った結果、最終ステップ(ある層の最大層間変形角が1/30時点)時においても、上層部に未崩壊層(降伏ヒンジが生じない階)が残った場合を想定します。
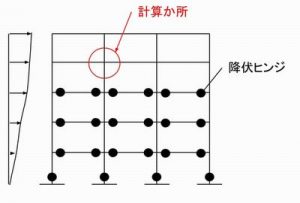
最終ステップ時(Rmax=1/30)降伏ヒンジ
2.接合部の余耐力計算
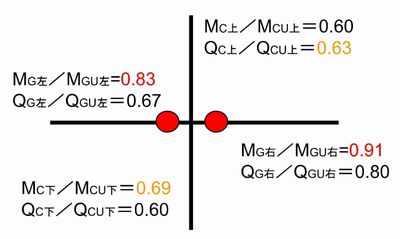
赤丸で囲まれた接合部について、余耐力法で崩壊形形成時の応力を算定します。
最終ステップにおける、接合部の応力状態と、接合部に取りつく部材の耐力が、下図で示す数値だった場合
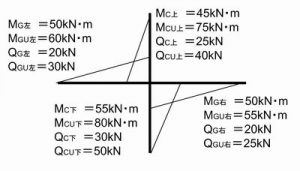
最終ステップ時の応力
各部材の、最終ステップ時の応力と体力の比を取ります。
MG左(右):左(右)側の梁の最終ステップ時の曲げモーメント
MGU左(右):左(右)側の梁の曲げ耐力
QG左(右):左(右)側の梁の最終ステップ時のせん断力
QGU左(右):左(右)側の梁のせん断耐力
MC上(下):上(下)側の柱の最終ステップ時の曲げモーメント
MGU上(下):上(下)側の柱の曲げ耐力
QG上(下):上(下)側の柱の最終ステップ時のせん断力
QGU上(下):上(下)側の柱のせん断耐力
3.崩壊形の想定
最終ステップ時の応力/耐力 を計算し、接点における各部材の耐力余裕度(1.0で破壊)を比較します。
①各部材の曲げ余裕度とせん断余裕度を比較し、大きい方を採用する(赤・オレンジ)
②部材同士の余裕度を比較し、大きい方から2つの部材が破壊すると想定する(赤)
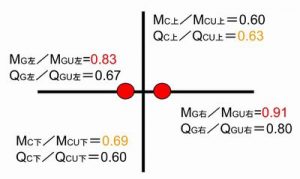
この接合部では、両側の梁が曲げ破壊を起こすと想定して、柱・梁の部材ランクを決定します。
(上の柱はせん断破壊、下の柱は曲げ破壊が先行すると考えられます。)
部材ランクの決定には崩壊形形成時の応力が必要なので、各部材の応力を、最終ステップ時の応力から増大させる必要があります。
例えば、上図では左右の梁が崩壊することを想定しているので、左右の梁の余裕度の合計の逆数 2/(0.83+0.91)=1.149を各部材の最終ステップ時の応力に掛けて、崩壊形形成時の応力とするなどの方法が考えられます。
以上、必要保有水平耐力算定時の課題、余耐力法の計算方法とその具体例について計算例をご紹介しました。
詳しい情報は、こちらの本を参考にしてください。