【土のφ、qu、C、Vs】N値から算定できます

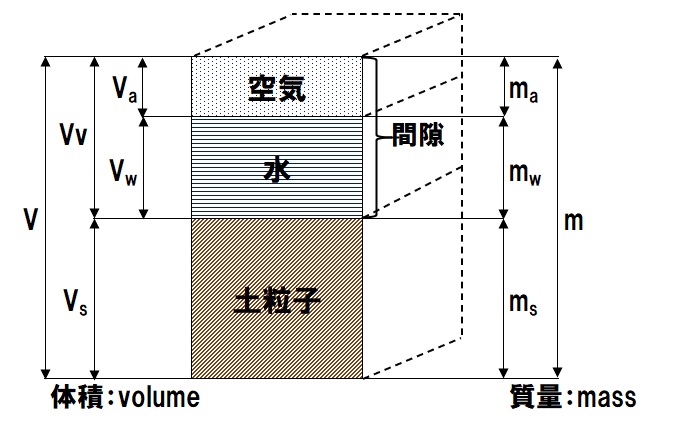
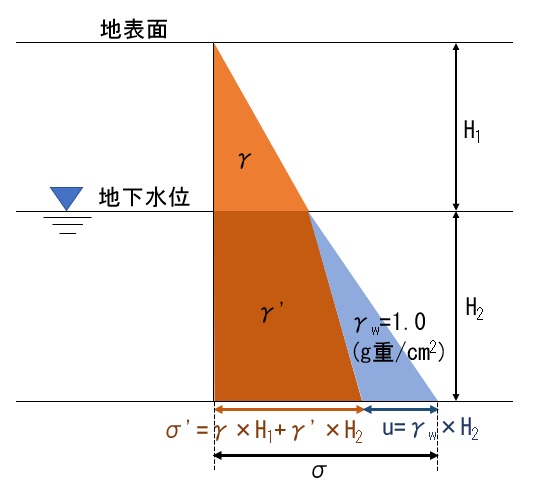
地盤の力学的性質は【N値】から計算可能

N値から算定できる力学的性質

• 内部摩擦角φ（°）
• １軸圧縮強度q_u（kN/m²）
• 粘着力C（kN）_{※quから計算する}
• せん断(S)波速度V_S（m/s）

• せん断弾性係数G（kN/m²）

• 粗密(P)波速度V_P（m/s）
• ヤング係数E（kN/m²）

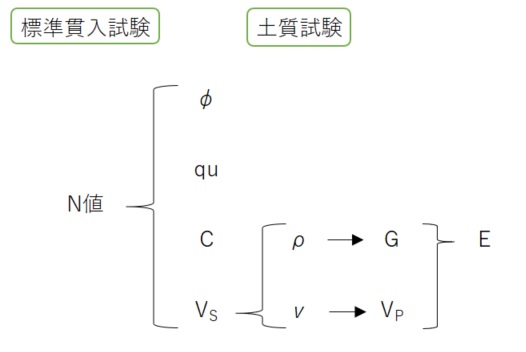
Coffee Break①

N値と内部摩擦角φの関係式

$$\phi=\sqrt{{20N}}+15{°}{・・・大崎式}$$
$$\phi=\sqrt{{15N}}+15{°}{・・・道路橋示方書}$$

N値と１軸圧縮強度quの関係式

$${q}_{u}=12.5{N}{(kN/{m}^2)}{・・・Terzaghi-Peck式}$$
$${q}_{u}=40+5{N}{(kN/{m}^2)}{・・・大崎式}$$
$${q}_{u}={(25～50)}{N}{(kN/{m}^2)}{・・・港湾基準式}$$
$${q}_{u}=25{N}{(kN/{m}^2)}{・・・地盤工学会式}$$

quと粘着力Cの関係式

$${C}=\frac{1}{2}{q}_{u}{(kN/{m}^2)}$$

N値とせん断波速度VSの関係式

今井式

$${V}_{S}=80.6{N}^{0.331}{(沖積砂質土:As)}$$
$${V}_{S}=102{N}^{0.292}{(沖積粘性土:Ac)}$$
$${V}_{S}=97.2{N}^{0.323}{(沖積粘性土:Ac)}$$
$${V}_{S}=114{N}^{0.292}{(沖積粘性土:Ac)}$$

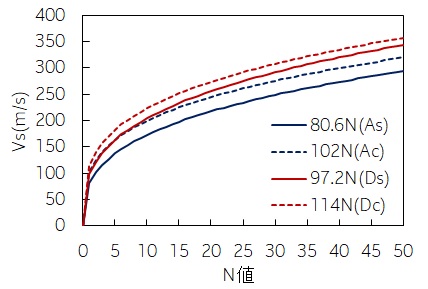
算定式を比較した図

道路橋示方書

$${V}_{S}=80{N}^{\frac{1}{3}}{(1≦N≦50)(砂質土)}$$
$${V}_{S}=100{N}^{\frac{1}{3}}{(1≦N≦25)(粘性土)}$$

鉄道標準式

$${V}_{S}=80{N}^{\frac{1}{3}}{ (1≦N≦50) (砂質土)}$$
$${V}_{S}=100{N}^{\frac{1}{3}}{(1≦N≦25)(粘性土)}$$
$${V}_{S}=23{{q}_{u}}^{0.36}{(2＜N)(粘性土)}$$

Coffee Break②

せん断弾性係数Gの関係式

$${G}=\rho{{V}_{S}}^2$$

$${V}_{S}=\sqrt{\frac{{G}}{{\rho}}}$$

ヤング係数Eの関係式

$${E}=2{G}{(1+\nu)}$$

粗密(P)波速度VPの関係式

$${V}_{P}=\sqrt{\frac{{E(1-\nu)}}{\rho{(1+\nu)(1+2\nu)}}}$$

VPとVSの関係式

$$\frac{{V}_{S}}{{V}_{P}}=\sqrt{\frac{1-2\nu}{2{(1-\nu)}}}$$

$$\nu=\frac{1-2{\left(\frac{{V}_{S}}{{V}_{P}}\right)^2}}{2\{1-{\left(\frac{{V}_{S}}{{V}_{P}}\right)^2\}}}$$

以上です。今回まとめた記事が、少しでも役に立てば幸いです。