【受動土圧と主動土圧】モールの応力円と土圧の評価式

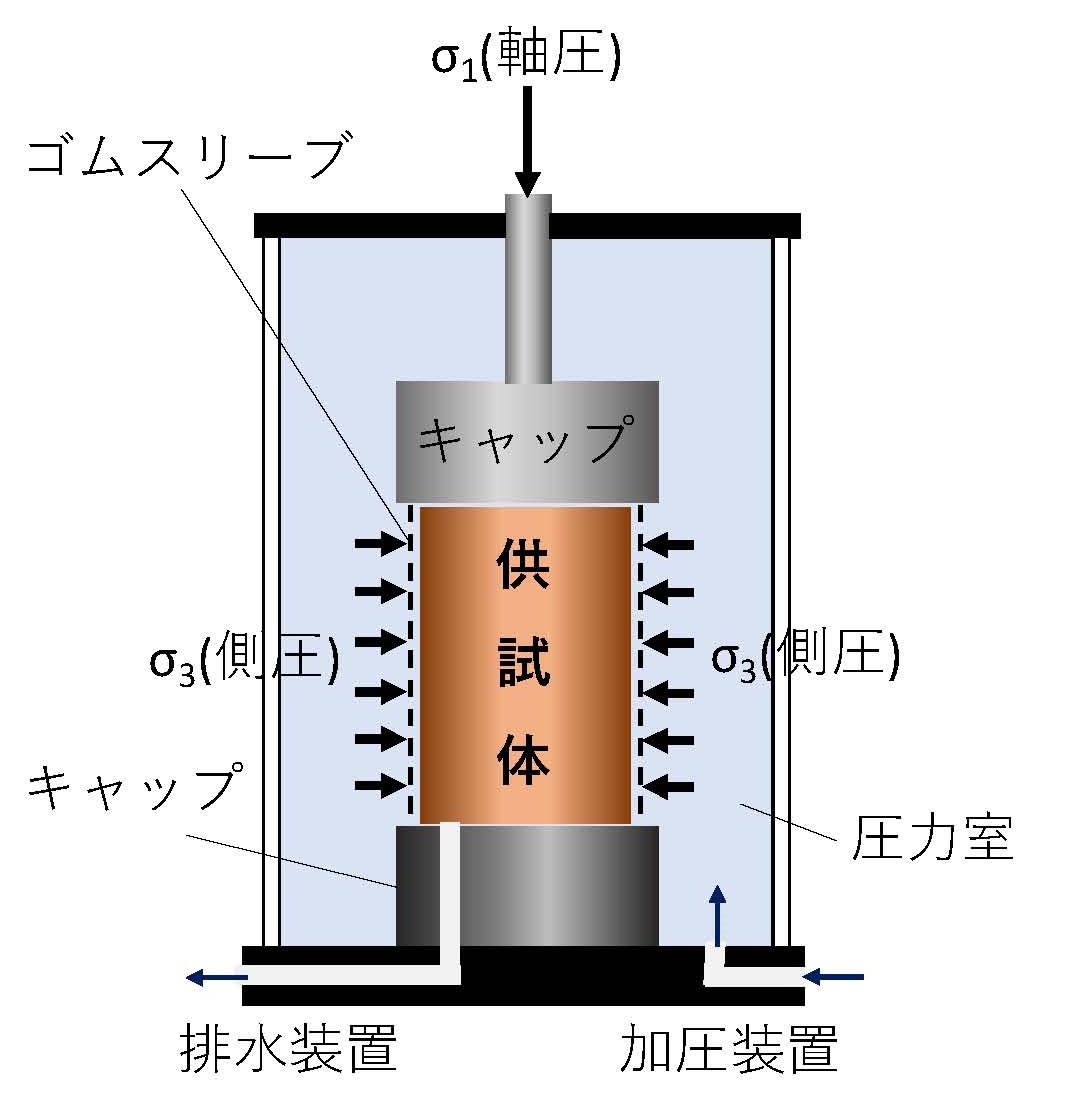
　このページでは、受働土圧と主働土圧について、モールの応力円とクーロンの破壊戦の図から、評価式を求める方法についてまとめています。

受動土圧と主動土圧

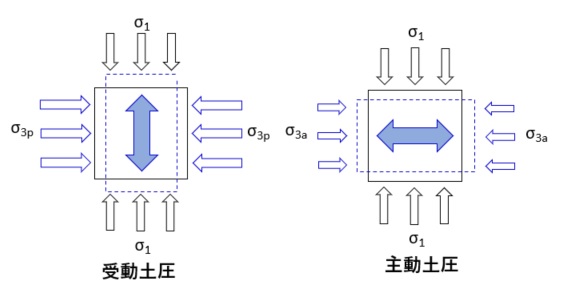
受動土圧

　受動土圧は、鉛直方向の応力(上載圧)σ₁が一定の条件で、これ以上、側圧が大きくなると、水平方向の応力が勝って破壊する限界の土圧σ_3pを言います。
受動土圧による土の破壊は、縦に変形して破壊します。

主動土圧

　主動土圧は、鉛直方向の応力(上載圧)σ₁が一定の条件で、これ以上、側圧が小さくなると、鉛直方向の応力が勝って破壊する限界の土圧σ_3aを言います。
主動土圧による土の破壊は、横に変形して破壊します。

受動土圧の評価式

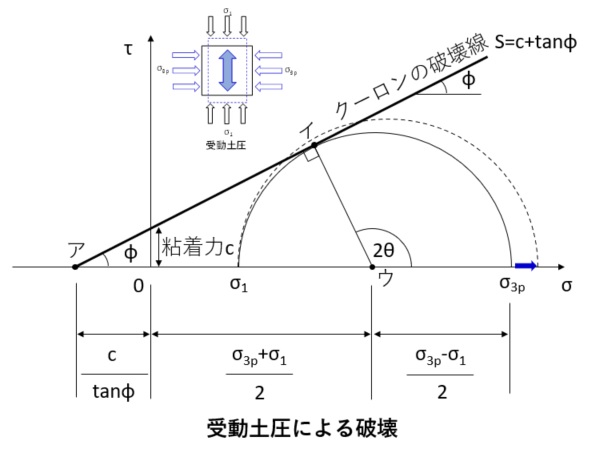
　受動土圧の評価式は、上の図のモールの応力円とクーロンの破壊線の関係から導くことができます。「三角形アイウ」の幾何学的な関係から、下式が成立します。

$$\left(\frac{C}{\tan{\phi}}+\frac{\sigma_{3p}+\sigma_{1}}{2}\right)\sin{\phi}=\frac{\sigma_{3p}-\sigma_{1}}{2}$$

これを整理すると

$$\left(1+\sin{\phi}\right)\sigma_{3p}=\left(1-\sin{\phi}\right)\sigma_{1}+\frac{\sin{\phi}}{\tan{\phi}}2{C}$$

更に整理すると、受動土圧は、以下の関係となります。

$$\sigma_{3p}=\frac{(1+\sin{\phi})}{(1-\sin{\phi})}\sigma_1-\frac{2\cos{\phi}}{(1-\sin{\phi})}{C}$$

主動土圧の評価式

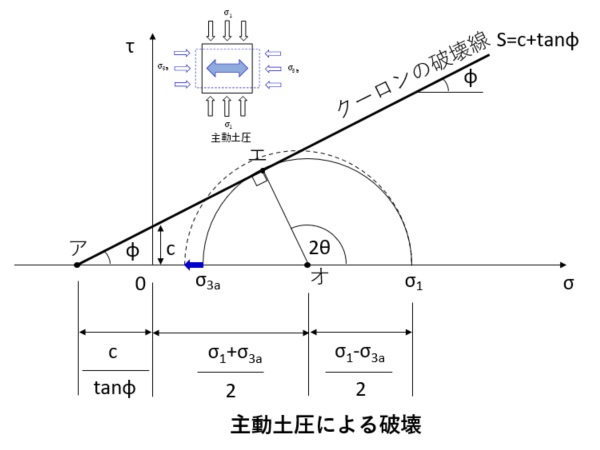
　主動土圧の評価式は、上の図のモールの応力円とクーロンの破壊線の関係から導くことができます。「三角形アエオ」の幾何学的な関係から、受動土圧と同じように整理すると、主動土圧は、以下の関係となります。

$$\sigma_{3p}=\frac{(1-\sin{\phi})}{(1+\sin{\phi})}\sigma_1-\frac{2\cos{\phi}}{(1+\sin{\phi})}{C}$$

例題

　内部摩擦角φ=10°，粘着力C=30kN/m²のシルト質地盤がある。地下水位は地表面下2mの位置にあり、それ以浅の単位体積重量は1.8ton重/m³で、それ以深の単位体積重量は2.0ton重/m³である。
①このときの地下10mにおける鉛直応力(有効応力)を求めよ。
②このときの地下10mの受動土圧と主動土圧を求めよ。
（※有効応力の求め方は、こちらのページを参照）