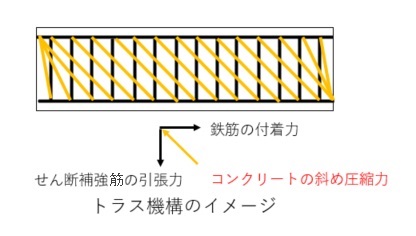
ここでは、RC梁部材の「せん断ひび割れ強度Qc」と「せん断終局強度Qsu」について式を示します。
せん断ひび割れ強度Qc=大野・荒川式
大野・荒川式
$$Q_{c}=\left(\frac{0.085k_{c}({F}_{C}+500)}{M{/}{(Qd)}+1.7}\right){bj}{(kgf)}$$
kc:部材せいに対する補正係数(d>40cmのとき、0.72)
Fc:コンクリートの圧縮強度(kgf/cm2)
M/(Qd):シアスパン比
b:部材幅(cm)
j:応力中心距離(=7d/8)(cm)
d:有効せい(cm)
※圧縮強度が60N/mm2以下の範囲までが適用範囲
せん断終局強度Qsu=荒川min式とmean式
せん断終局強度Qsuを求める式には、荒川min式と荒川mean式の2つがあります。
mean=平均、min=最小という意味です。
荒川min式
荒川min式は、長方形断面のはりについて単調増加載荷で行われたせん断実験の結果を元につくられたせん断終局強度式です。実験強度が荒川min式を下回る確率は5%以下で、ほぼせん断終局強度の下限値が得られます。
$$Q_{su}=\left(\frac{0.053{{p}_{t}}^{0.23}{(F_{C}+18)}}{M{/}{(Qd)}+0.12}+0.85\sqrt{{P}_{w}\sigma_{wy}}\right){bj}{ (N)}$$
荒川mean式
荒川mean式は、実験値/計算値の平均値は全体で1.32で、変動係数は0.24、基準値の1.0に対して±30%以内に含まれるデータは、全体の48.77%です。
$$Q_{su}=\left(\frac{0.068{{p}_{t}}^{0.23}{(F_{C}+18)}}{M{/}{(Qd)}+0.12}+0.85\sqrt{{P}_{w}\sigma_{wy}}\right){bj}{ (N)}$$
pt:引張鉄筋比(%)
Fc:コンクリートの圧縮強度(N/mm2)
M/Q:M、Qはそれぞれ終局強度算定時における部材内の最大モーメントおよびせん断力(ただし、M/(QD)は、M/(Qd)<1のとき1とし、M/(Qd)>3のとき3とする)
d:はり有効せい(mm)
pw:せん断補強筋比(小数、中子筋を除く場合0.012を上限とする。ただし、せん断補強筋として中子筋を併用する場合やスパイラル筋を用いる場合にはを上限とすることができる。)
σwy:せん断補強筋の降伏強度(N/mm2)
b:はり幅(mm)
j:応力中心間距離で7d/8としてよい(mm)
荒川min式と荒川mean式のイメージ
実験値/計算値の関係から、実験値が標準正規分布に従うと仮定して、頻度分布で表現してみました。
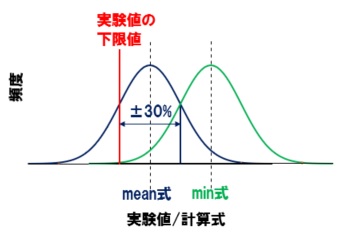
荒川min式で実験値を割ると、実験強度が式を下回る確率が5%なので、グラフの緑色の線になります。
荒川mean式で求めた実験値を割ると、実験強度が式を下回る確率は25.7%となります。荒川mean式のグラフでは、実験値の下限値が、算定式より下回る可能性が25.7%となることを示しています。
ただし、荒川mean式で求めた実験値/計算値が1.30を超えるものが多くあったことや、式を構成するコンクリート強度Fc、せん断補強筋の降伏強度σwyについて、計算で使用する値と比べると、実際には1.1倍程度であることを考慮すると、安全側に評価できます。
以上、RC部材のせん断強度に関する式についてご紹介しました。