梁・ばねモデルの基本式
梁・ばねモデルの基本式は、次のように表されます。
$${EI}\frac{{d}^4y}{{dx}^4}+{Bk}_{h}y+Ky=w$$
E:山留め壁材料のヤング係数(kN/m“)
I:単位幅あたりの山留め壁の断面2次モーメント(m4)
y:山留め壁の水平変位(m)
x:深さ(m)
B:単位幅(m)
kh:水平地盤反力係数(kN/m3)
w:単位幅あたりの荷重(kN/m)
K:切梁軸方向のばね定数
$$K=\alpha\frac{2{E}_{k}{A}_{k}}{al}$$
α:切梁の緩みを表す係数(α=0.5~1.0:ジャッキ等で緩みがない場合α=1.0)
Ek:切梁のヤング係数(kN/m2)
Ak:切梁の有効断面積(ボルト孔考慮)(m“)
a:切梁の水平間隔(m)
l:切梁の長さ(掘削幅)(m)
梁・ばねモデルの基本式の導出方法
山留壁の設計では、梁・ばねモデルが用いられます。切梁を用いた山留め壁の梁・ばねモデルを下図に示します。
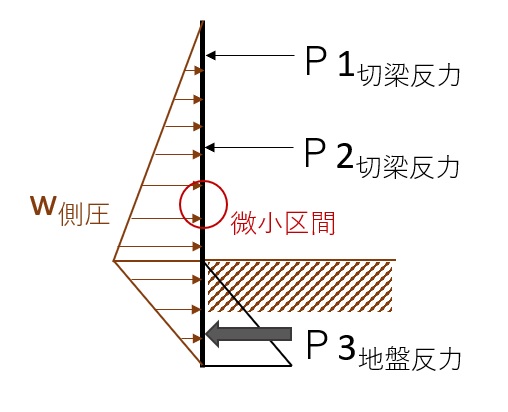
梁・ばねモデル
梁・ばねモデルの基本式は、梁の曲げに関する微分方程式で、山留壁に上の図のように応力が作用している場合の、微小区間について応力のつりあいを考えます。
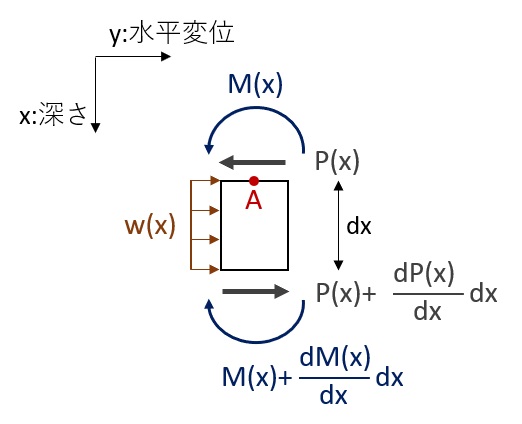
微小区間の応力状態
y方向の力のつりあい
図のy方向の力のつりあいを考えると、次の式で表すことができます。
$$-P(x)+w(x)dx+P(x)+\frac{dP(x)}{dx}dx=0$$
A点まわりのモーメントのつりあい
図のA点における、時計回りを正(+)としたモーメントのつり合いを考えると、次の式で表すことができます。
$$-M(x)-w(x)dx\frac{dx}{2}-(P(x)+\frac{dP(x)}{dx}dx)dx+(M(x)+\frac{dM(x)}{dx}dx)=0$$
ここで微小量と考え、\(w(x)dx\frac{dx}{2}\)や\((\frac{dP(x)}{dx}dx)dx\)は微小量の2乗なので、0として整理します。
整理したy方向のつりあい式
$$\frac{dP(x)}{dx}+w(x)=0{・・・式1}$$
整理したA点まわりのモーメントのつりあい式
$$P(x)=\frac{dM(x)}{dx}{・・・式2}$$
式1をxで微分すると
$$\frac{dP(x)}{dx}=\frac{{d}^2M(x)}{d{x}^2}{・・・式3}$$
式2と式3より、曲げに関するつり合い式を次のように表します。
$$\frac{{d}^2M(x)}{d{x}^2}+w(x)=0{・・・式4}$$
ここで、弾性曲線法の基本式より
$$\frac{{d}^2y}{d{x}^2}=-\frac{M(x)}{EI}$$
$$\begin{eqnarray}
M(x) &=& -{EI}\frac{{d}^2y}{d{x}^2} \\
\frac{{M(x)}^2}{{d}^2x} &=& -{EI}\frac{{d}^4y}{d{x}^4}{・・・式5}
\end{eqnarray}$$
式4と式5から
$$-{EI}\frac{{d}^4y}{d{X}^4}+w(x)=0{・・・式6}$$
山留め壁の梁・ばねモデルへの展開
式6をもとに、w(x)と反対方向に働く、切梁反力と地盤反力を単位幅あたりの応力(wと同じ単位)で表すことで、梁・ばねモデルの式となります。
$${EI}\frac{{d}^4y}{{dx}^4}+{Bk}_{h}y+Ky=w$$
E:山留め壁材料のヤング係数(kN/m“)
I:単位幅あたりの山留め壁の断面2次モーメント(m4)
y:山留め壁の水平変位(m)
x:深さ(m)
B:単位幅(m)
kh:水平地盤反力係数(kN/m3)
w:単位幅あたりの荷重(kN/m)
K:切梁軸方向のばね定数
$$K=\alpha\frac{2{E}_{k}{A}_{k}}{al}$$
α:切梁の緩みを表す係数(α=0.5~1.0:ジャッキ等で緩みがない場合α=1.0)
Ek:切梁のヤング係数(kN/m2)
Ak:切梁の有効断面積(ボルト孔考慮)(m“)
a:切梁の水平間隔(m)
l:切梁の長さ(掘削幅)(m)
以上、梁・ばねモデルの基本式についてでした。