現在価値?n年後?
診断士試験では、n年後の工事費用を現在価値に換算する。という問題が出題されますが、いったい何のことでしょうか。私なりに考えてみました。
まずは、一般的な複利計算から
複利計算は、一般的に借金をしたときに返済すべき金額の計算に使われます。複利の計算方法は下式の通りです。
$$返済額=借りた金額×(1+複利)^{返済期間}$$
例えば、年複利2%で1000万円を借り、10年後に返済するとします。その場合
$$10年後の返済額=1000万×(1+0.02)^{10}=約1219万円$$
となります。
現在価値の計算方法
現在価値の考え方は、上の複利計算の逆過程だと考えてください。つまり、複利計算の式を変形させて、n年後の価値から、現在の価値を逆算するということになります。
$$n年後の価値=現在価値×(1+社会的割引率)^{n}$$
$$現在価値=\frac{n年後の価値}{(1+社会的割引率)^{n}}$$
いきなり逆を考えると分かりにくいので、複利計算と同じような考えで、「橋を造る」ことの価値を時間軸で考えてみます。

例えば100億円で高架橋を造るとします。高架橋としての価値は、人や物が往来できることにあります。そう考えると、今から使えるのと、将来使えるのでは価値が異なってきます。
人や物が往来できると、それに伴って経済活動も活発になり、橋を使えることによる価値が年々増えていきます。それが年2%だったりするわけです。
つまり、早く高架橋を造り10年後に経済発展した場合と、単に10年後に高架橋をつくるのでは、高架橋としての価値が違うわけです。
この考え方は、複利計算(借金返済)の考え方と似ていて、現在いくら払ったら、〇〇年後には〇〇円になっていますという考え方です。
社会的割引率とは
n年後の価値に社会的割引率を考慮して、現在価値に換算するという手法のため、割引という言葉が入っていますが、筆者としては
n年後の価値の計算=複利計算から式を変形
する方がしっくりきますので、社会的割増率の方がふさわしいのではと思ってしまいます。
割引率というと、n年後にはインフレなのかデフレなのかによって、現在のお金の価値が変わってしまうため、あくまでもモノを主体として考えると割増率が正しいのではと思うからです。(これは、単に覚え易いという意味であり、正確な定義を言っているのではありません。)
診断士過去問2014-No.39
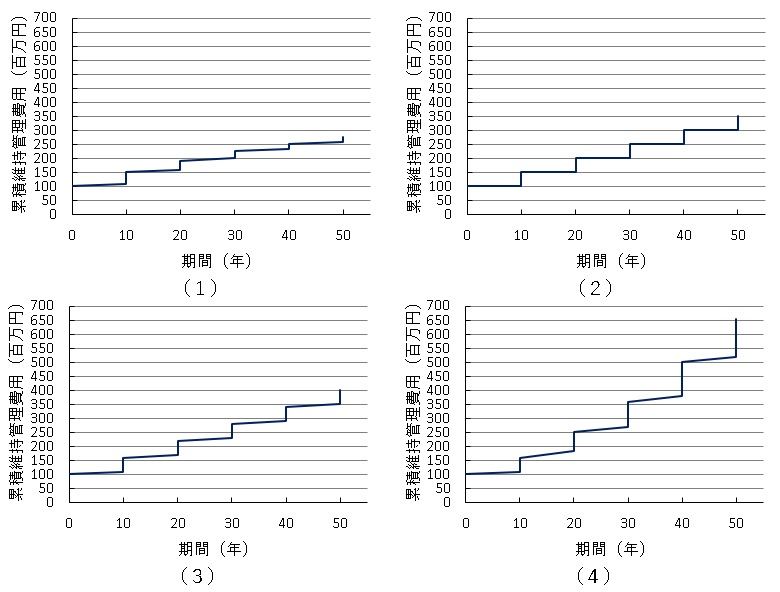
塩害環境下に建設した鉄筋コンクリート構造物に対して、予防保全を前提として表に示す維持管理のシナリオを設定した。建設後50年間の維持管理費用の推移を示した次の(1)~(4)の図のうち、適当なものはどれか。ただし、維持管理費用には建設時の表面被覆工法の工事費用も含む。
| 表 設定した維持管理シナリオ | |
| 建設時に表面被覆工法を適用することとし、その補修頻度は10年ごとに1回とする。 | |
| 建設時の表面被覆工法の工事費用 | 100百万円 |
| 1回あたりの補修費用 | 50百万円 |
| 毎年点検を実施することとする。 | |
| 年間の点検費用 | 1百万円 |
| 社会的割引率 | 2.0% |
クリックして【2014―No.39】の解答と解説をみる
正解(1)
累積維持管理費用は、今後50年間を10年毎に同じ補修を繰り返す費用を現在価値に換算します。そのため、10年ごとの補修費用が少しずつ下がっている(1)が正解です。
例えば、10年後、20年後の費用を現在価値に換算すると下のような式になります。
$$現在価値=\frac{{50百}}{(1+0.02)^{10}}=41$$
$$現在価値=\frac{{50百}}{(1+0.02)^{20}}=33$$
また、2010―No.47では、現在価値の計算式そのものが出題されています。
診断士過去問2010-No.47
n年後に実施を予定している補修工法の費用を複利法によって現在価値に換算する式として次のうち適当なものはどれか。
正解は・・・\(現在価値=\frac{n年後の補修費}{(1+\gamma)^{n}}\)
以上、LCCについてまとめました。これで1点を取れるようにしましょう!