\(\sqrt{t}\)則とは?
コンクリートの中性化速度を表すものです。
コンクリート構造物の、コンクリート表面からの中性化深さの進行は、経過年数の平方根で表すことができます。式で表すと、以下になります。
$${d}=\alpha\sqrt{t}$$
d:中性化深さ(mm)
α:中性化速度係数
t:経過時間(年)
このページでは、コンクリート診断士試験の問題を参考に、\(\sqrt{t}\)則の解説をしていきます。
中性化深さの式”\(\alpha\sqrt{t}\)”の計算で注意したいこと
問題例1(2001年No.29)
竣工後25年が経過したコンクリート構造物において、コンクリートの中性化深さを調査したところ15mmであった。竣工後50年が経過した時点での中性化深さの予測値として適当なものはどれか。
- 約15mm
- 約20mm
- 約30mm
- 約60mm
中性化深さの推定式はルートt則で行います。
$$中性化深さ=α\sqrt{t}$$
αは係数で、測定結果から逆算して求めます。
tは経過年数で、単位は通常「年」を用います。
この問題では、15 = α × √ 25から、 α = 3を算出してから
50年後の中性化深さ = 3 × √ 50 ≒ 20 という計算手順になります。この問題は、素直に中性化深さの推定式に数値を当てはめていけばよいので、引っ掛かるところはありません。
問題例2(2009年No.27)
竣工年が不明な打放しコンクリート構造物の中性化深さを測定したところ15mmであった。この構造物の16年前の中性化深さは9mmであった。この構造物の竣工年からの経過年数に関する次の推定値のうち、適当なものはどれか。ただし、環境条件は変わらず、中性化深さの進行は経過年数の平方根に比例すると仮定する。
- 25年
- 44年
- 64年
- 100年
まず、√t側での計算結果を記載します。ここで、注意しなけらばならないのは、中性化深さの進行は、直線的ではないということです。
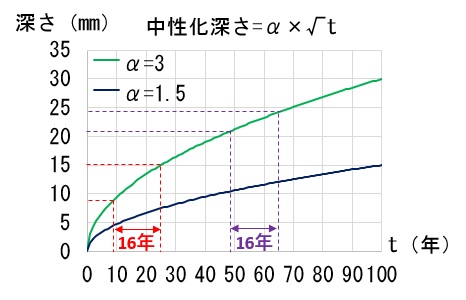
この問題でいうと、16年の期間を経過年数のどの期間で取るかということが答えに影響してきます。
そのために、「竣工年が不明」とあるので、まずは竣工後 x年 経過していると仮定し、そこから√t則の式に当てはめていきます。
15 = α × √x
9 = α × √(x – 16)
上記2式を解くことにより、α = 3と竣工経過年数 x = 25 が算出されます。
このひっかけに注意
単に、16年の経過で、15 – 9 = 6mm という計算をすると α = 1.5 となり、xは 100年 となってしまいます。
なんと、選択肢4.に100年もありますね!焦らず、きっちりと問題を解けば引っ掛からないと思いますので、ご注意ください。
問題例3(2014年No.22)
建設後20年を経過したコンクリート打放し仕上げの外壁について、中性化深さを調査したところ、平均値22mm、標準偏差9mmとなった。
この外壁のかぶり(厚さ)は40mmであるとして、建設後40年経過後に、中性化深さがかぶり(厚さ)を超える確率として、次の(1)~(4)のうち適当なものはどれか。
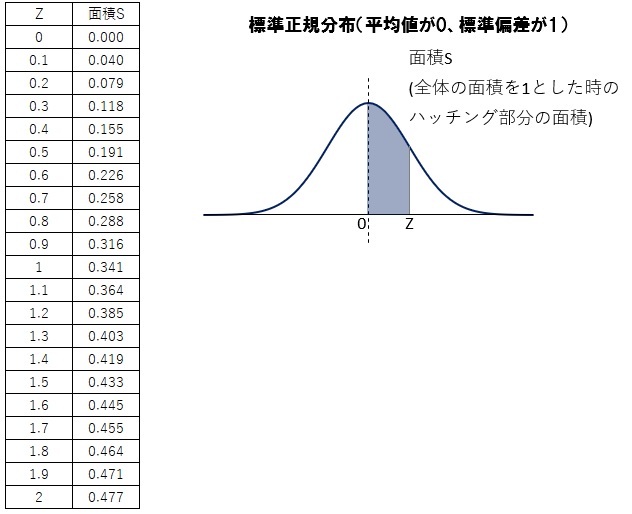
なお、中性化深さの分布は正規分布と見なしてよい。また、計算に当たっては、以下の標準正規分布を用いてよい。ただし、中性化の進行は√t則に従うものとし、今後、環境条件、中性化深さの変動係数は変化しないものとする。
- 約16%
- 約24%
- 約32%
- 約48%
回答例
まずは、建設後40年経過した際の中性化深さを算出します。20年経過後の数値は問題文にありますので、そこからまずはαを出しましょう。√t則のαは中性化深さの平均値から算出します。
22 = α √20
α = 22 / √2
建設後40年では、、、
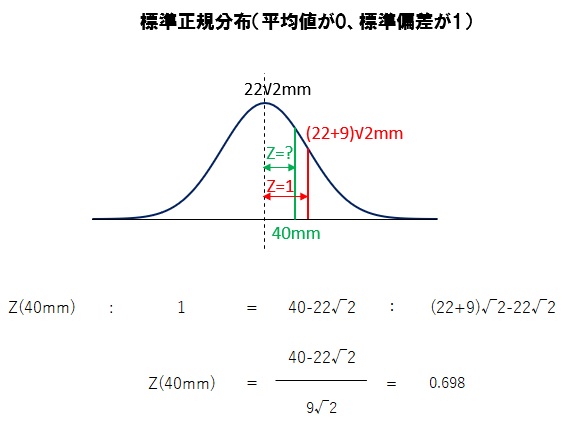
tμ(40年経過後平均値) = (22 / √2)√40 = 22√2 mm
tσ(40年経過後標準偏差) = (9 / √2)√40 = 9√2 mm
ここから、正規分布の問題です。
建設後40年経過した際の平均値を正規分布上のセンターと考えます。
その標準偏差1の場合のかぶり厚さは tμ + tσ として考えかぶり厚40mmの時のZを求めます。
Z=0.7(≒0.698)の時の面積S(Z=0.7)はS=0.258です。
ここで、面積Sは、全体の面積を1とした時のハッチングした部分の面積でしたね。かぶりを”超える”確率は、Z=0.7の右側の部分の面積になります。
S(Z=0.7よりも右側) = 1(全体の面積) - S(Z=0.7よりも左側)= 1(全体の面積) -(S(Z=0.7) + 0.5)
つまり、0.5 - 0.258 = 0.242
約24%で答えは(2)となります。
正規分布に基づく問題は、上図を思い浮かべて解いていきましょう!