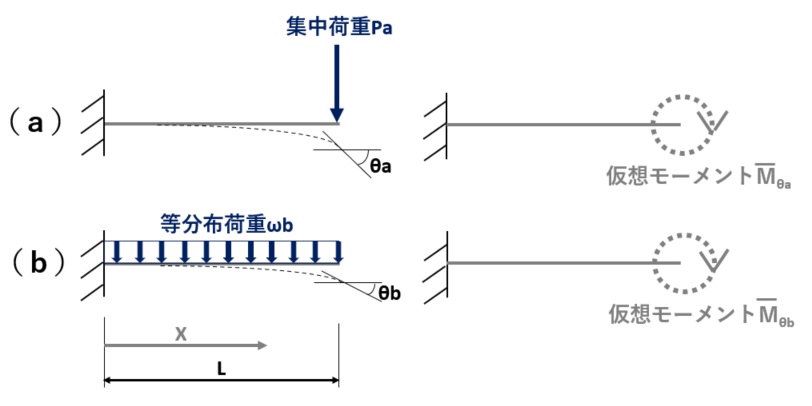
部材各部の曲げモーメントの大きさ\(M_x\)から、部材に蓄えられるひずみエネルギーUは次式で求められます。
$$U=\int_{0}^{L}\frac{M_x^2}{2EI}dx$$
L:部材長
E:ヤング係数
I:中立軸に関する断面2次モーメント
<解説と図解>
幅dxの梁の微小要素に蓄えられるひずみエネルギーdUは次式となります。
$$dU=dW_e=\frac{M_xd\theta}{2}$$
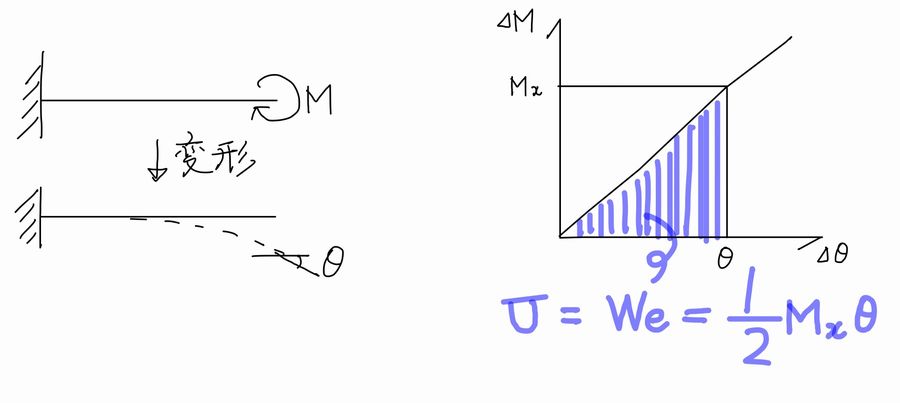
また、\(d\theta=\frac{M_x}{EI}dx\)より
$$U=\int_{0}^{L}dU=\int_{0}^{L}\frac{M_xd\theta}{2}=\int_{0}^{L}\frac{M_x^2}{2EI}dx$$
<さらに詳しく解説> \(d\theta=\frac{M_x}{EI}dx\)について
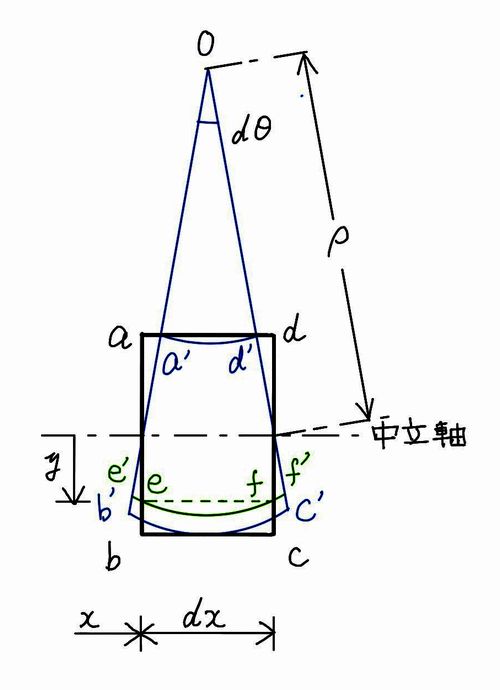
中立軸からyだけ離れた\(\overline{ef}\)の長さは、変形後\(\overline{e’f’}\)となります。上図より
$$\overline{ef}=dx=\rho d\theta$$
$$\overline{e’f’}=(\rho+y)d\theta$$
その部分のx方向の変形量を\(\Delta\)とすると
$$\Delta=\overline{e’f’}-\overline{ef}=(\rho +y)d\theta-\rho d\theta=yd\theta$$
よって、ひずみ度\(\varepsilon=\frac{\Delta L}{L}\)は
$$\varepsilon=\frac{\Delta}{dx}=\frac{yd\theta}{\rho d\theta}=\frac{y}{\rho}$$
また、フックの法則(\(\sigma=E\varepsilon\))と\(\sigma=\frac{M}{I}y\)より
$$\varepsilon=\frac{\sigma}{E}=\frac{M_x}{EI}y$$
上式\(\varepsilon\)は等しく\(\frac{y}{\rho}=\frac{M_x}{EI}y\)なので
$$\frac{1}{\rho}=\frac{M_x}{EI}$$
上図は微小変形を対象としているため、角度\(\tan\theta=\theta\)が成り立つので
$$d\theta=\frac{dx}{\rho}$$
よって
$$d\theta=\frac{dx}{\rho}=\frac{M_x}{EI}dx$$
ひとつずつ式を追っていくと、等式で成り立つことがわかりますね!\(\sigma=\frac{M}{I}y\)については、次回詳しく書いていこうと思います。