RC部材の構造解析を行う際、多くの場合は、せん断変形を考慮せずに行いますが、FEM解析等で詳細検討する際やせん断変形が無視できない場合には、【形状係数κ】を用います。
構造解析ソフトやRC規準を参照しても、矩形断面の形状係数が1.2(6/5)であるとの結論は書いてありますが、導出過程がなかなかわかりませんでした。
この導出過程について、一番腑に落ちた研究内容がありましたので、ざっくりと紹介します。
引用元:小野里健一;せん断変形を求めるための形状係数に関する研究(日本建築学会構造系論文集,第84巻,第762号)
せん断応分布についての概説
梁部材に、曲げによって生じるせん断応力 τ は、曲げ応力 σ と異なり、梁の中立軸位置で最大となる非線形分布となることが知られています。
曲げ応力は中立軸位置で対象となる線形の分布であるため、計算が簡単ですが、せん断応力は非線形分布であるため計算が煩雑になります。これが、形状係数kを用いる理由です。
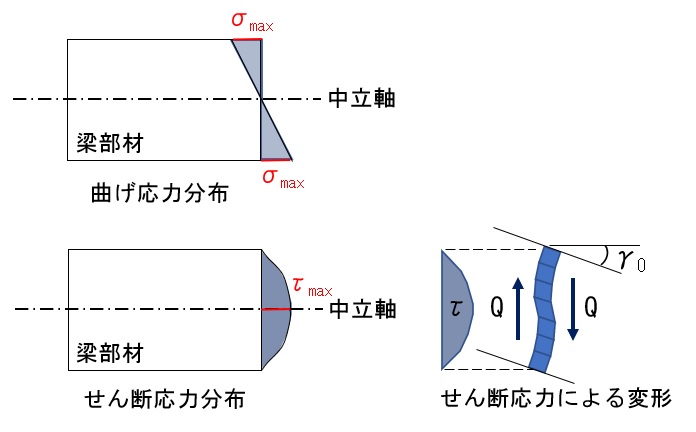
せん断変形角とせん断応力の関係
梁断面内に生じる応力とひずみの関係式を立式します。
・せん断応力 τ
・せん断ひずみ γ
・せん断弾性係数 G
とすると、フックの法則より、以下の式となります。
$$\tau={G}{\gamma}$$
ここで、Timoshenkoの梁理論から、曲げによって生じる最大せん断応力τmaxと平均せん断応力τmeanの比は、せん断【形状係数κ】と呼ばれます。
$${k}=\frac{\tau_{max}}{\tau_{mean}}$$
平均せん断応力τmeanは、梁部材の断面積Aとせん断力Qの関係から下式で表せます。
$$\tau_{mean}=\frac{Q}{A}$$
A:はりの断面積
Q:せん断力
以上から、τmaxは下式
$$\tau_{max}={k}\frac{Q}{A}$$
フックの法則の式にτmax、G、γ0をそれぞれ代入して変形すると。
$$\gamma_0=\frac{{k}{Q}}{{A}{G}}$$
となります。
せん断応力分布と変形の関係
曲げを受ける梁部材の、せん断応力のみによる変形は下図のようにS字となります。
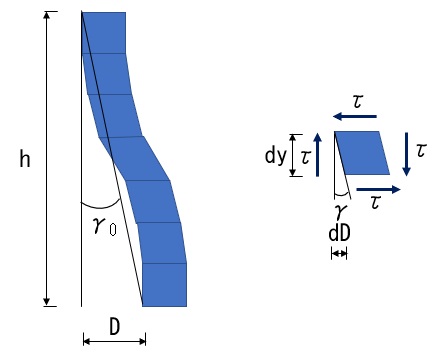
せん断応力による変形で生じる部材の回転をγ0とすると左の図より
$$\gamma_0=\frac{D}{h}$$
右の微小区間のせん断変形図から
$$dD={\gamma}{dy}$$
DとdDの関係は、
$$D=\int_{-y_1}^{y_2}{dD}$$
\(\gamma=\frac{\tau}{G}\)を用いて
$$D=\frac{1}{G}\int_{-y_1}^{y_2}\tau{dy}$$
\(\gamma_0=\frac{D}{h}\)であったので
$$\gamma_0=\frac{1}{Gh}\int_{-y_1}^{y_2}\tau{dy}$$
\(\gamma_0=\frac{kQ}{AG}\)より
$$k=\frac{A}{Qh}\int_{-y_1}^{y_2}\tau{dy}$$
せん断応力分布の数式表現
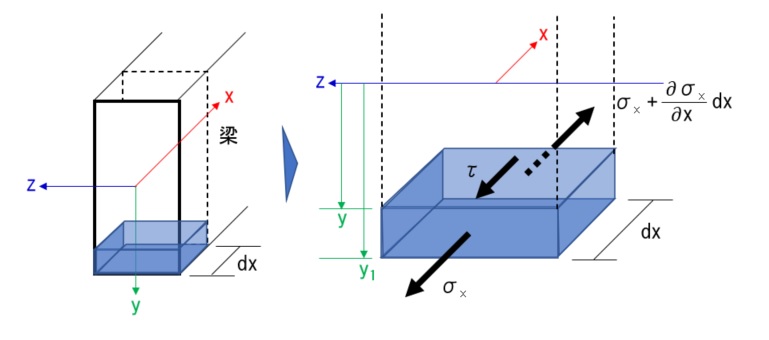
まず、上の図のように矩形断面(梁)の微小面積について、x方向の力のつり合いを求めます。材軸方向がx軸です。$$-\int_{y}^{y1}\int_{0}^{b(y)}{\sigma_{x}}dzdy-\int_{0}^{b(y)}({\tau}dx)dz+\int_{y}^{y1}\int_{0}^{b(y)}({\sigma}_{x}+\frac{\partial{\sigma}_{x}}{\partial}xdx)dzdy$$
次に、積分の足し算は分解できることを利用すると、1項目の数式が消えます。$$-\int_{0}^{b(y)}{({\tau}dx)dz+\int_{y}^{y1}\int_{0}^{b(y)}\frac{\partial{\sigma}_{x}}{\partial}x}dxdzdy=0$$
\int_{0}^{b(y)}({\tau}dx)dz &=& \int_{y}^{y1}\int_{0}^{b(y)}\frac{\partial{\sigma}_{x}}{\partial}xdxdzdy\\
\int_{0}^{b(y)}{\tau}dz &=& \int_{y}^{y1}{b(y)}\frac{\partial{\sigma}_{x}}{\partial}xdy
\end{eqnarray}$$
軸方向ひずみは平面保持の過程より、yの原点が断面の中心にあると考えると、下の式になります。$$\varepsilon_{x}=\varepsilon_{0}+\kappa{y}$$
N &=& \int_{A}^{}\sigma_{x}dA=\varepsilon_0{EA}{\space;\space\space}A=\int_{A}^{}dA\\
M &=& \int_{A}^{}{y}\sigma_{x}dA=\kappa{E}\int_{A}^{}{y}^2dA=\kappa{E}{I}_{z}{\space;\space\space}{I}_{z}=\int_{A}^{}{y}^2dA
\end{eqnarray}$$
上の式から$$\varepsilon_0=\frac{N}{EA}{\space;\space\space}\kappa=\frac{M}{E{I}_{z}}$$
これを、σxの式に代入すると$$\sigma_{x}=\frac{N}{A}+\frac{M}{{I}_{z}}y$$
ここで準備計算として、σxをxで偏微分します。軸力は、材軸方向で一定のため、軸力の項は定数項を微分すると考え、0になります。つまり、曲げモーメントの項のみ考慮すると、次の式になります。ここで、曲げモーメントMを軸方向に微分するとせん断力Qになる(M=Qx)ことを使います。$$\frac{\partial{\sigma_{x}}}{\partial{x}}=\frac{y}{{I}_{z}}\frac{dM}{dx}=\frac{y}{{I}_{z}}Q{\space;\space\space}\frac{dM}{dx}=Q$$
に、σxを微分した式を代入します。S(y)はz軸に対する断面一次モーメントを表します。$$\int_{0}^{b(y)}{\tau}dz=\int_{y}^{y1}\frac{yQ}{{I}_{z}}b(y)dy=\frac{Q}{{I}_{z}}S(y){\space;\space\space}S(y)=\int_{y}^{y1}yb(y)dy$$
\int_{0}^{b(y)}{\tau}dz &=& \tau{b(y)}=\frac{Q}{{I}_{z}}S(y)\\
\tau &=& \frac{Q}{{I}_{z}b(y)}{S(y)}
\end{eqnarray}$$
ここで、せん断応力τは、共益の関係であるため、材軸方向と、材軸直行方向のせん断応力は等しいです。つまり、上の式から、断面のy方向のせん断応力分布が求められることになります。
矩形断面だとするとτの分布はS(y)を求めることで算出できます。
$$\begin{eqnarray}
S(y) &=& -\int_{y}^{\frac{D}{2}}ybdy={B}{\left[\frac{{y}^2}{2}\right]}_{y}^{\frac{D}{2}}=\frac{b}{2}\left(1-{\left(\frac{2y}{D}\right)}^2\right)\\
&=& \frac{b{D}^2}{8}\left(1-{\left(\frac{2y}{D}\right)}^2\right)
\end{eqnarray}$$
これを、τ(y)の式に代入すると$$\tau=\frac{Q}{{I}_{z}b}\left(1-{\left(\frac{2y}{D}\right)}^2\right)\frac{b{D}^2}{8}=\frac{3Q}{2A}\left(1-{\left(\frac{2y}{D}\right)}^2\right)$$
せん断力分布は、断面の中央部で最大値τmaxをとるので、y=0を代入すると
$$\tau_{max}=\kappa\frac{Q}{A}=\kappa\tau_{0}{\space;\space\space}\kappa=1.5{\space;\space\space}\tau_0=\frac{Q}{A}$$
せん断応力分布の式からせん断形状係数を求める
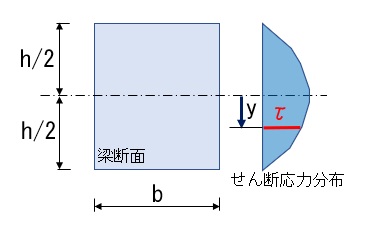
ここからは、図のように、幅b、せいhの梁(矩形)断面を考えます。梁せい方向はy方向です。せん断応力の式は次のように表しました。
$$\tau=\frac{3Q}{2A}\left(1-{\left(\frac{2y}{D}\right)}^2\right)$$
ここに、A=bh、D=hを代入し、式を変形すると
$$\tau=\frac{6Q}{bh^3}((\frac{h}{2})^2-y^2)$$
となります。
$$k=\frac{A}{Qh}\int_{-y_1}^{y_2}\tau{dy}$$
にτを代入すると
$$k=\frac{A}{Qh}\int_{-h/2}^{h/2}\frac{6Q}{bh^3}((\frac{h}{2})^2-y^2)dy=1$$
となり、1.2となりません・・・。
せん断形状係数が1.2となる考え方
仮想仕事法のように、内力と外力のつり合い式で解く方法です。
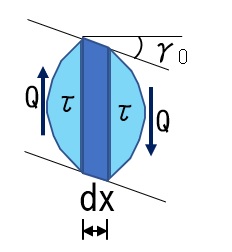
上図のように、微小区間のせん断力とせん断変形関係から
$$dWe=\frac{1}{2}Q\gamma_0dx$$
dWe:外力仕事
せん断応力分布τに従った変形角をγとすると、内力仕事dWiは
$$dW_{i}=\frac{1}{2}\int_{-y_1}^{y_2}\tau(bdy)(\gamma{dx})=\frac{1}{2}(\int_{-y_1}^{y_2}b\tau\gamma{dy}){dx}$$
\(\gamma=\frac{\tau}{G}\)を代入すると
$$dW_{i}=\frac{1}{2G}(\int_{-y_1}^{y_2}b{\tau}^2dy)dx$$
外力仕事dWe=内力仕事dWiより
$$\frac{1}{2}Q\gamma_0dx=\frac{1}{2G}(\int_{-y_1}^{y_2}b{\tau}^2dy)dx$$
$$\gamma_0=\frac{1}{QG}\int_{-y_1}^{y^2}b{\tau}^2dy$$
\(\gamma_0=\frac{kQ}{AG}\)の関係から
$$k=\frac{A}{{Q}^2}\int_{-y_1}^{y_2}b{\tau}^2dy$$

図のような矩形断面の時\(\tau=\frac{6Q}{bh^3}((\frac{h}{2})^2-y^2)\)だったので
$$k=\frac{A}{{Q}^2}\int_{-h/2}^{h/2}b(\frac{6Q}{bh^3}{({(\frac{f}{2})}^2-{y}^2))}^2dy=\frac{6}{5}$$
矩形断面の形状係数は1.2となります。
どうやら、RC規準もこのような考え方で形状係数を決定しているということでしょうか。今後も学習を続けて、情報を発信したいと思います。ご存知の方は、コメントにてご教授の程お願い申し上げます。以上