建築物が地震による水平力を受ける場合、下図のような曲げ応力が生じることを仮定して、構造計算が行われます。
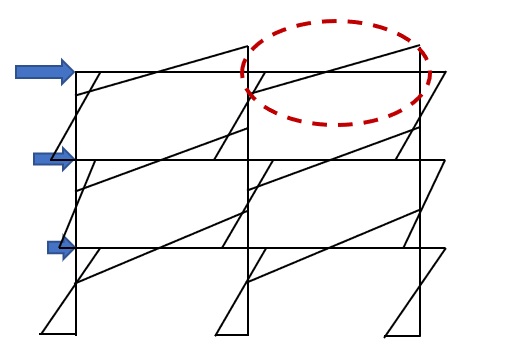
今回の記事では、この時の梁部材に着目し、どのようなモデル化がなされているかを見ていきます。
梁部材のモデル化
重さを支えるために梁にかかる応力とは異なり、水平力を受けた場合の曲げモーメントの分布図と部材の変形は、下図のようになります。
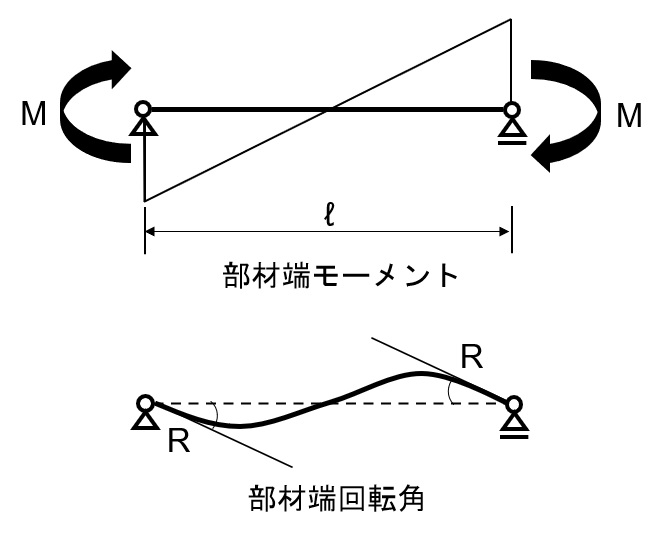
梁部材は、ピン-ローラー支承でモデル化されます。構造解析では、部材をばねに置き換えて計算が行われます。ばねとは「力-変形」の関係を持つものだと思ってください。これを部材の復元力特性とも言います。
梁部材のモデル化では以下の関係となります。
- 力=曲げモーメント
- 変形=回転
梁部材には、軸力とせん断力も同時に働きます。
軸力については通常、梁部材の解析では考慮しません。曲げモーメントやせん断力に対して、問題にならないくらい小さい軸力である場合が多いからです。一歩、柱部材では、建物の自重を支えている状態のため、軸応力も考慮します。
せん断力については、考慮はします。しかし、部材をせん断破壊させると、脆性的な破壊(バサッと壊れる)が生じることになり、万が一の安全性を確保できません。そこで、構造解析では、曲げ破壊が生じると仮定した場合に生じるせん断力に対して、余裕のある断面とします。したがって、梁部材は生じるせん断力に対しては余裕のある設計を行い、先に曲げ破壊を生じさせることで、粘り強い構造とすることが基本となります。
つまり、梁部材については、部材の曲げに対して詳細に検討を行うことが必要ということになります。
話を戻しますと、地震による水平力を受けた場合の梁部材には、下図のような曲げ応力がはたらきます。そこから、梁部材のばねのモデル化は、両端に同じ方向の曲げモーメント(図では時計回り)が生じた場合の回転角との関係を表すものとなります。
ここで、RC部材は下記の過程を経て、剛性が低下していきます。
- 平面保持のかていによる初期剛性
- ひび割れによる剛性低下
- 主筋の降伏による剛性低下
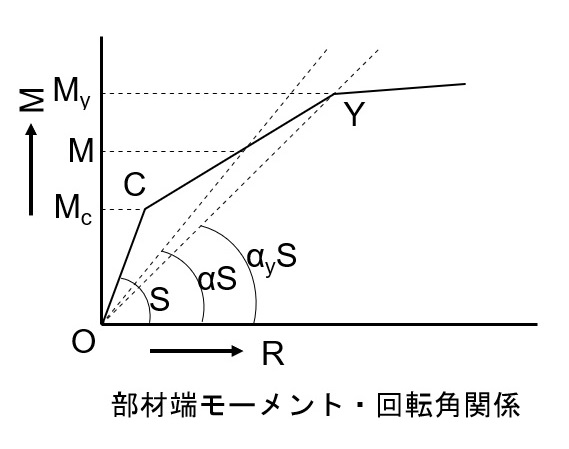
図の折れ点「C」でひび割れ、「Y」で主筋の降伏が生じる点です。
①初期剛性の計算方法
$$S=\frac{M}{R}=\frac{6EI}{\ell}$$
②ひび割れモーメントMcの計算方法
$$M_{c}=0.56\sqrt{\sigma_{b}}{Ze}$$
σb:コンクリートの圧縮強度(N/mm2)
Ze:断面係数
③降伏モーメントMyの計算方法
$$M_{y}=a_{t}\sigma_{y}j_{t}$$
ここで、jtを0.9dとして、次式として考えても良いとされています。
$$M_{y}=0.9a_{t}\sigma_{Y}$$
at:引張鉄筋の断面積(mm2)
σy:鉄筋の降伏強度(N/mm2)
d:梁の有効せい(mm)
④降伏時の剛性低下率
$$\alpha_{y}=(0.043+1.64np_{t}+0.043\frac{a}{D}){(\frac{d}{D})}^2$$
n:ヤング係数比
pt:at/(bD)
b:梁幅
D:梁せい
d:梁の有効せい
a:シアスパン長さ,a=M/Q
M:曲げモーメント
Q:せん断力
ここで、αは「剛性低下率」と言い、Mc、Myおよび降伏点Yにおける剛性低下率αyから推定することが出来ます。
以上、①~④の計算方法で、復元力特性は求めることが出来ると思いますので、今回はここまでです。この記事はすべてRC規準を引用しています。詳細を学びたい方はRC規準を見てください。
引用元:鉄筋コンクリート構造計算規準・同解説,2018-日本建築学会-