弾性衝撃波法の計算問題について、分かりにくい点を自分なりにまとめました。
<2016年No.14>
図1に示すように、コンクリート表面から空隙までの深さを弾性衝撃波法によって推定する。センサー1で測定された波形を周波数分析した結果、図2に示す周波数スペクトルが得られた。また、図3には、センサー1およびセンサー2で測定された波形の0~50μsまでを拡大しており、弾性波の到達時刻を読み取った値も示している。このとき、コンクリート表面から空隙までの深さの推定値として、次の(1)~(4)のうち最も適当なものはどれか。ただし、センサー1とセンサー2の中心間距離は100mmである。
- 120mm
- 125mm
- 240mm
- 250mm
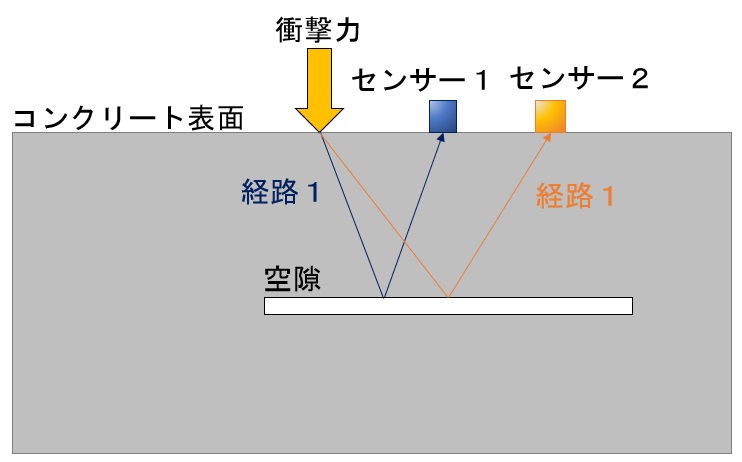
図1
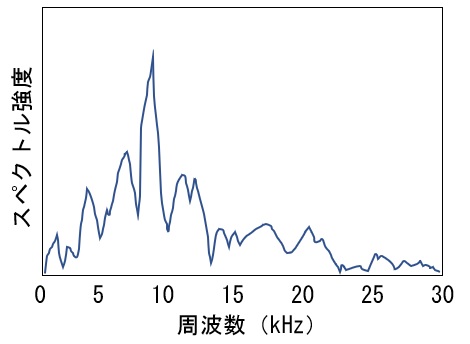
図2
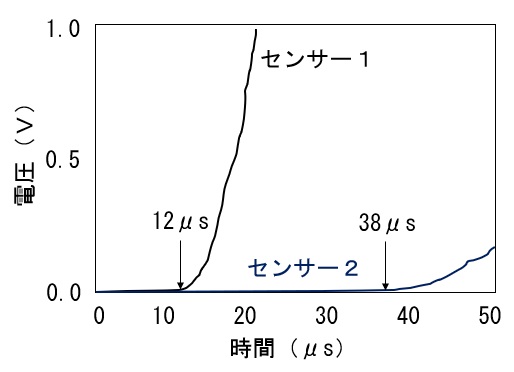
図3
解説によると、d=V/2f の関係式による。とありますが、何のことか、覚えにくいなっていう方は、この先もお読みください。
d=V/2fを表現した図
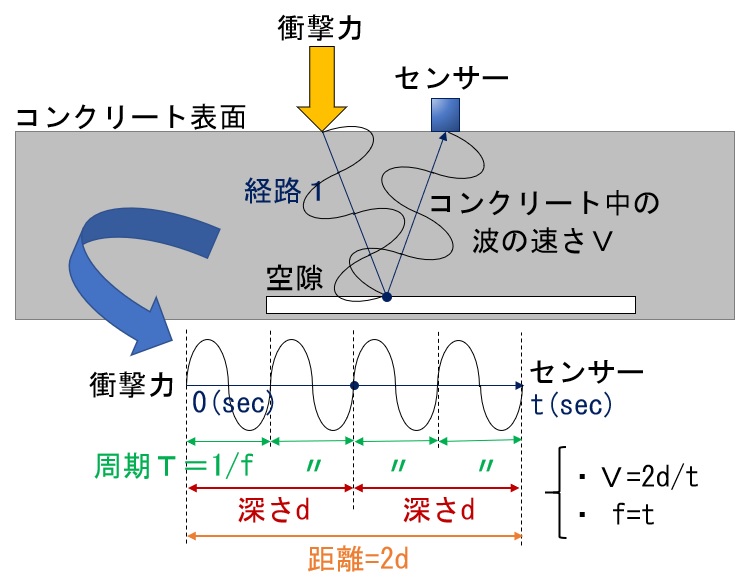
分かりやすくするために、センサーをひとつにしました。
衝撃が与えられると、その衝撃は波としてコンクリート中を伝わります。縦波ですが、表現上は分かりやすく横波っぽく描いてます。
コンクリート中の空隙に波がぶつかると、反射して返ってくるという図になります。ここで、衝撃を与えてから最も強いスペクトルの周波数f(図2)が、センサーに返ってくるまでの時間をt秒とします。すると、コンクリート中の波の速さVは、波が行って帰ってくるまでの距離から、2d/tということになります。
$$\left\{\array{V&=\frac{2d}{t}\\t&=f}\right.$$
$$d=\frac{V}{2f}$$
さて、ここでコンクリート中の波の速度Vが分かれば、距離dがわかりそうですね。
図3のグラフを見ると、センサー1とセンサー2の電圧が変化し始める位置が分かります。この点は、衝撃を与えた点からコンクリートの表面を伝播した波がセンサーによって検出された点を差します。
ここで、センサー1とセンサー2の距離は100mmということが分かっていますので、コンクリート中の波の速度は、100/(38-12)(mm/μsec)ということになります。
この値を、d=V/2fに代入します。fは最も強いスペクトルの周波数、8kHzを代入します。
$$d=\frac{\frac{100}{26×10^{-6}}}{2×8000}=240.3846…$$
衝撃力を与えた点とセンサー1との距離は分かりませんが、ほぼ垂直に近いと判断できます。また、式の答えが240.3846…mmのため、それよりも少し小さい値をとることが推測できます。よって答えは(3)240mmです。
補足
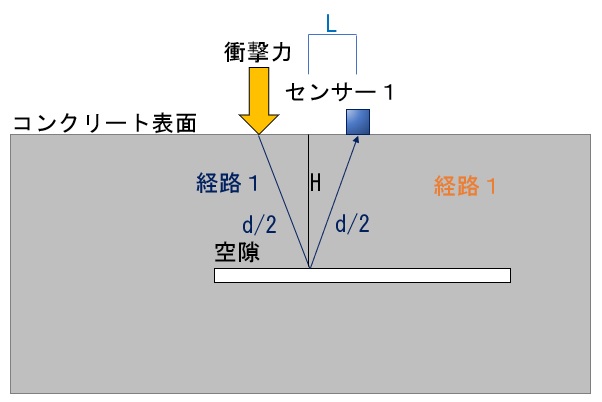
さて、d=240.3846…とありましたが、実際の深さは上の図のHに相当します。三平方の定理からHが求められるので、計算してみましょう。
$$H=\sqrt{{(\frac{d}{2})}^2-{L}^2}$$
$$H=\sqrt{(240.3846…)^2-({{\frac{100}{26×10^{-6}}}×(12×10^{-6}))^2}}$$
H=235.9122417…となってしまいました。
答えが240mmなので、これで正しいのか、ちょっと不安になりますが、空隙の上端か、中央かによっても変わりますし、選択肢で求められているのは”推定値”ですので、ここではおおよそ240mmということで納得しておきましょう。